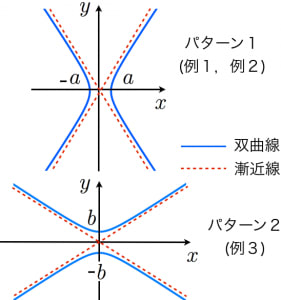
平方根の計算ルートの分数の足し算・引き算の仕方がわかる5ステップ 中1数学 162 簡単公式三角錐の表面積の求め方がわかる2ステップ 中1数学 中学数学球の体積の求め方の公式を1発で覚える方法 中3数学 169ここでは、双曲線の漸近線についてみていきます。 双曲線と漸近線 基本双曲線の焦点(焦点がx軸上)などで見た通り、2つの点(焦点)からの距離の差が、0でない一定の値になる点の軌跡を、双曲線といいます。 焦点が x 軸上漸近線の方程式 解説 高校の微分積分で漸近線の問題が登場するのは,微分法の応用として,「増減,極値,凹凸,変曲点,漸近線の方程式を求めてグラフの概形を書け」という場面です。 したがって,漸近線の方程式を単独で問うことはまれです。

指数関数とは何か 指数と関数の意味からわかるグラフの仕組みとその性質 アタリマエ
漸近線 求め方 ルート
漸近線 求め方 ルート-漸近線とは「しだいに近づいていく直線」のことです。 「しだいに近づいていく」をもう少しきちんと言うと「十分遠くで距離が限りなく $0$ に近づいていく」です。この説明でだけでは漸近線の意味が分かりにくいので、3つの具体的な漸近線のパターンを漸近線である。 漸近線の求め方 y=f(x) の漸近線がy ax b とすると,x が+∞ある いは-∞のとき,y の値はほぼ同じと考えられるので, f(x)≒ax+b ・・・① とおける。両辺をx で割って,lim計算すると, lim( ) ( ) lim x b a x f x x x よって, x f x a x ( ) lim


複雑な関数のグラフのかき方 数学 苦手解決q A 進研ゼミ高校講座
漸近線の求め方教えてください 数学 締切済 教えて!goo双曲線の漸近線について,具体例,簡単な導出方法,きちんとした証明を解説します。 例題 漸近線とは,関数が 原点から遠い部分で限りなく近づく直線 のことです。 まずは具体例から。漸近線を持つ代表的な関数 漸近線はない場合もありますし、複数ある場合もあります。 ですが漸近線を必ず持つとわかっている関数がいくつかあるので、最低限これらの関数は押さえておきましょう。 指数関数 \(y=2^x,y=2^{x}\)はグラフのようになりますが、\(x\)軸に着目すると漸近線である
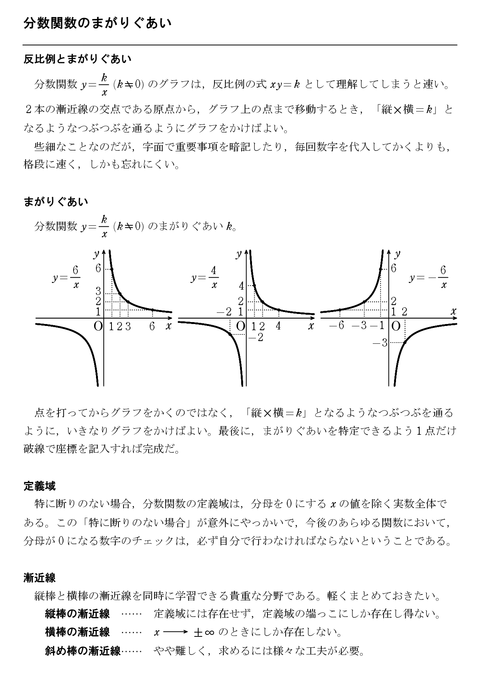
見て頂いてありがとうございます. 見てもらうために作成しておりますので,どんどん見てください.★の数は優先度です.★→★★→★★★ の順に取り組みましょう.3211←→ ポイント集をまとめて見たい場合 点線より下側の解き方 一般項が、不定形∞∞の形であるので、それを避けた形に変形する。 ルート記号があるときには、(この問題の場合は分子)有理化を考える。 ∞にしたときの極限は、比の形(分数の形)で求められることが多いので、分母に1があると思って変形し※この頁では漸近線の方程式の求め方を解説します. (1) 縦方向の( x 軸に垂直な)漸近線 有限の値 a に対して, x→a のとき y→∞ または y→−∞ になるとき, x=a が漸近線になります.
こんにちは、ウチダショウマです。 今日は、数学Ⅱで初めて登場するが詳しくは数学Ⅲで習う 「漸近線」 について、求め方、意味、定義について解説していきます! 主な具体例(分数関数や双曲線)も挙げながら詳しく見ていきましょう♪ 漸近線とは まずは聞き慣れない言葉だと思いますので漸近線、臨界点および変曲点を求める ライブ スクリプトを開く この例は、ある簡単な関数を解析して、漸近線、最大値、最小値、変曲点を見つける方法を説明します。手計算でやるならせいぜい $141$ まで。次の $1414$ なんて電卓がないとやる気が起こりません。本当に $\sqrt{2}$ の値を深く求めたいのであれば,やり方を変えた方がよさそうです。 図形から求める (中3) 直角をはさむ辺の長さが1の直角二等辺三角形を考え



Yvun1bpplsrahm


分数関数と無理関数のグラフ 漸近線 平行移動と方程式 不等式の解法
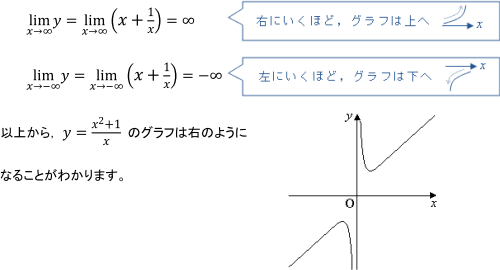
数学・算数 (e^2x1) / (e^x2) の漸近線を求めよという問題があります。 xはわかったのですが、 y軸と平行な漸近線の求め方がわかりません。 答えは y= 1/2のようです。手計算でやるならせいぜい $141$ まで。次の $1414$ なんて電卓がないとやる気が起こりません。本当に $\sqrt{2}$ の値を深く求めたいのであれば,やり方を変えた方がよさそうです。 図形から求める (中3) 直角をはさむ辺の長さが1の直角二等辺三角形を考え定数関数、多項式関数のグラフには、漸近線は存在しない。 漸近線が存在する最も簡単な例は、関数 f(x) = 1 / x のグラフである。 このグラフの漸近線は、直線 x = 0 と直線 y = 0 である。 グラフを描くと、曲線 y = 1 / x は x → 0±, x → ±∞ のときにそれぞれ y 軸、 x 軸に近づくことが見てとれる。


関数の漸近線を求める方法なんですけど したの画像のように式変形しないと Yahoo 知恵袋



指数関数とは何か 指数と関数の意味からわかるグラフの仕組みとその性質 アタリマエ
漸近線の求め方 初歩的な質問かもしれませんが、漸近線の導き出し方 がわかりません。 たとえば、 y=x^2/(x2) の概形をかけ。 という問題で、増減表で凹凸を調べ、与式が y=x24/(x2)と変形されるところまでは理解できたのですが、NTT データ数理システムでリサーチャーをしている大槻 (通称、けんちょん) です。今回は計算量オーダーの求め方について書きます。 0 はじめに 世の中の様々なシステムやソフトウェアはアルゴリズムによって支えられています。Qi漸近線の描き方を一目にまとめました。 漸近線とは、曲線が近づく直線のことをいい、x軸に平行な漸近線、y軸に平行な漸近線、y=mxnの形の漸近線の3種類があります。 単元 積分, キーワード 漸近線,分数関数,対数,指数,分数,双曲線,無理関数,傾き,切片,例題,解法,微分,極限,求め方,log,logarithm



双曲線の知識まとめ 焦点 漸近線 方程式 媒介変数表示 接線公式 理系ラボ


漸近線の方程式
漸近線の求め方を解説しました。 グラフの漸近線は、x軸に垂直な漸近線とそうでない漸近線とがあります。 そうでない漸近線は、\(x\to\pm\infty\)において漸近線と曲線が限りなく近づきます。 漸近線の方程式を\(y=axb\)とすると、曲線\(y=f(x)\)の漸近線は、ここでは、双曲線の漸近線についてみていきます。 双曲線と漸近線 基本双曲線の焦点(焦点がx軸上)などで見た通り、2つの点(焦点)からの距離の差が、0でない一定の値になる点の軌跡を、双曲線といいます。 焦点が x 軸上定数関数、多項式関数のグラフには、漸近線は存在しない。 漸近線が存在する最も簡単な例は、関数 f(x) = 1 / x のグラフである。 このグラフの漸近線は、直線 x = 0 と直線 y = 0 である。 グラフを描くと、曲線 y = 1 / x は x → 0±, x → ±∞ のときにそれぞれ y 軸、 x 軸に近づくことが見てとれる。



ルート関数の中身が二次 Y X 2 1 1まで に入ります のグラフはど 数学 教えて Goo



新入試対応 数学iii基礎問題精講 四訂新装版 上園信武 本 通販 Amazon


関数の値域 定義域 漸近線の求め方 1 Y 2 3 Yahoo 知恵袋



漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学


授業での雑談ネタ 怜悧玲瓏 高校数学を天空から俯瞰する



驚くばかり ルート の 微分 公式 画像ブログ



漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学


双曲線の漸近線の簡単な求め方と証明 高校数学の美しい物語


複雑な関数のグラフのかき方 数学 苦手解決q A 進研ゼミ高校講座
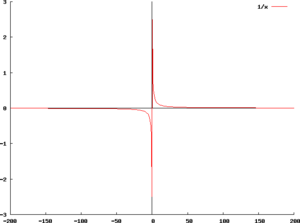


漸近線 Wikipedia



双曲線とは 式の導出とグラフ 漸近線までイラストでわかりやすく解説



分数関数とは グラフや微分 積分 不等式の解き方 受験辞典



分数関数のグラフ 反比例と平行移動 高校数学の知識庫
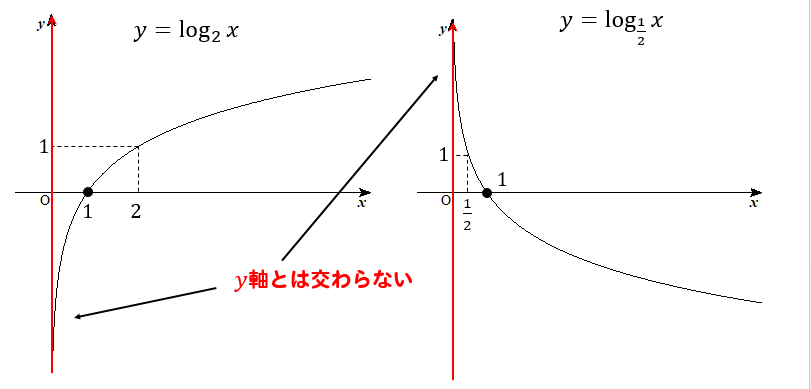


Logのグラフ 書き方を解説 平行移動の場合には 数スタ
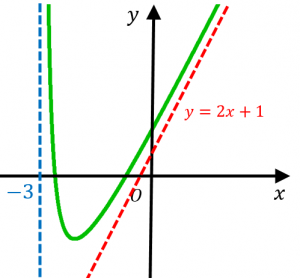


漸近線の求め方3パターン 具体例で学ぶ数学


高校数学 分数関数のポイント整理 双曲線と漸近線 偏差値40プログラマー



微分をしてグラフを描く問題で確認するポイント 数学 微分 そーまのブログ屋さん



極限のとりかたは理解しているなぜ無限大に極限をとったときと負 高校数学に関する質問 勉強質問サイト



Logの積分ですが Okwave
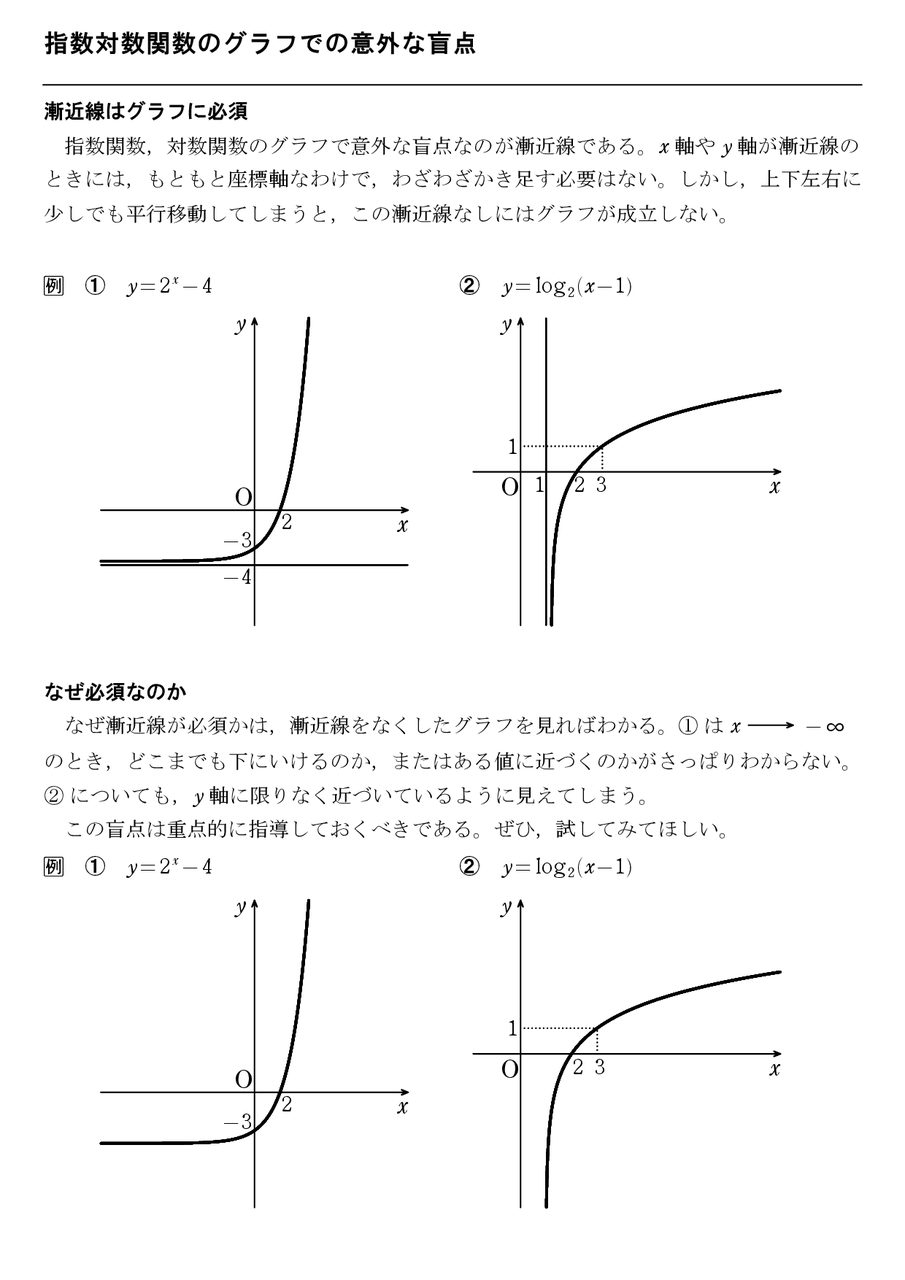


16年06月 怜悧玲瓏 高校数学を天空から俯瞰する



漸近線の方程式がy 2x 5 Y 2x 3で 点 1 1 を通る双曲線の方程式を その他 教育 科学 学問 教えて Goo



平成の東大理系数学 1995年 ちょぴん先生の数学部屋



指数関数とは何か 指数と関数の意味からわかるグラフの仕組みとその性質 アタリマエ



漸近線とは 求め方 高校数学 Youtube



分数関数のグラフ 反比例と平行移動 高校数学の知識庫



漸近線を調べて 概形をかけ という問題です 漸近線を求めると 高校数学に関する質問 勉強質問サイト



漸近線 Wikipedia



複雑な関数のグラフのかき方 数学 苦手解決q A 進研ゼミ高校講座


分数関数と無理関数 数 けけどう Note



分数関数とは グラフや微分 積分 不等式の解き方 受験辞典



基本 双曲線と漸近線 なかけんの数学ノート


反比例とは グラフの描き方や式の求め方をわかりやすく解説します Studyplus スタディプラス



双曲線の知識まとめ 焦点 漸近線 方程式 媒介変数表示 接線公式 理系ラボ



数3グラフの符号についてです Clear



Y Tan8のグラフの書き方 三角関数のグラフ 数学ii By ふぇるまー マナペディア



漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学


比例と反比例の関数のグラフの形や座標などのまとめ
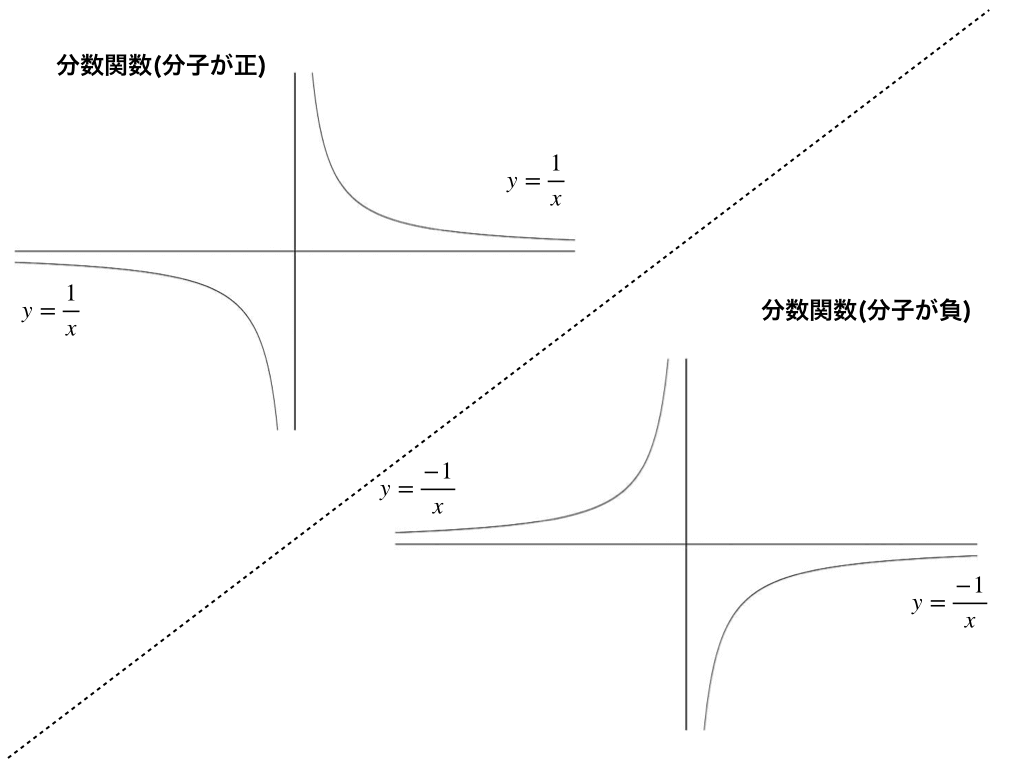


分数関数と無理関数のグラフ 漸近線 平行移動と方程式 不等式の解法



Y Tan8のグラフの書き方 三角関数のグラフ 数学ii By ふぇるまー マナペディア


漸近線 Wikipedia
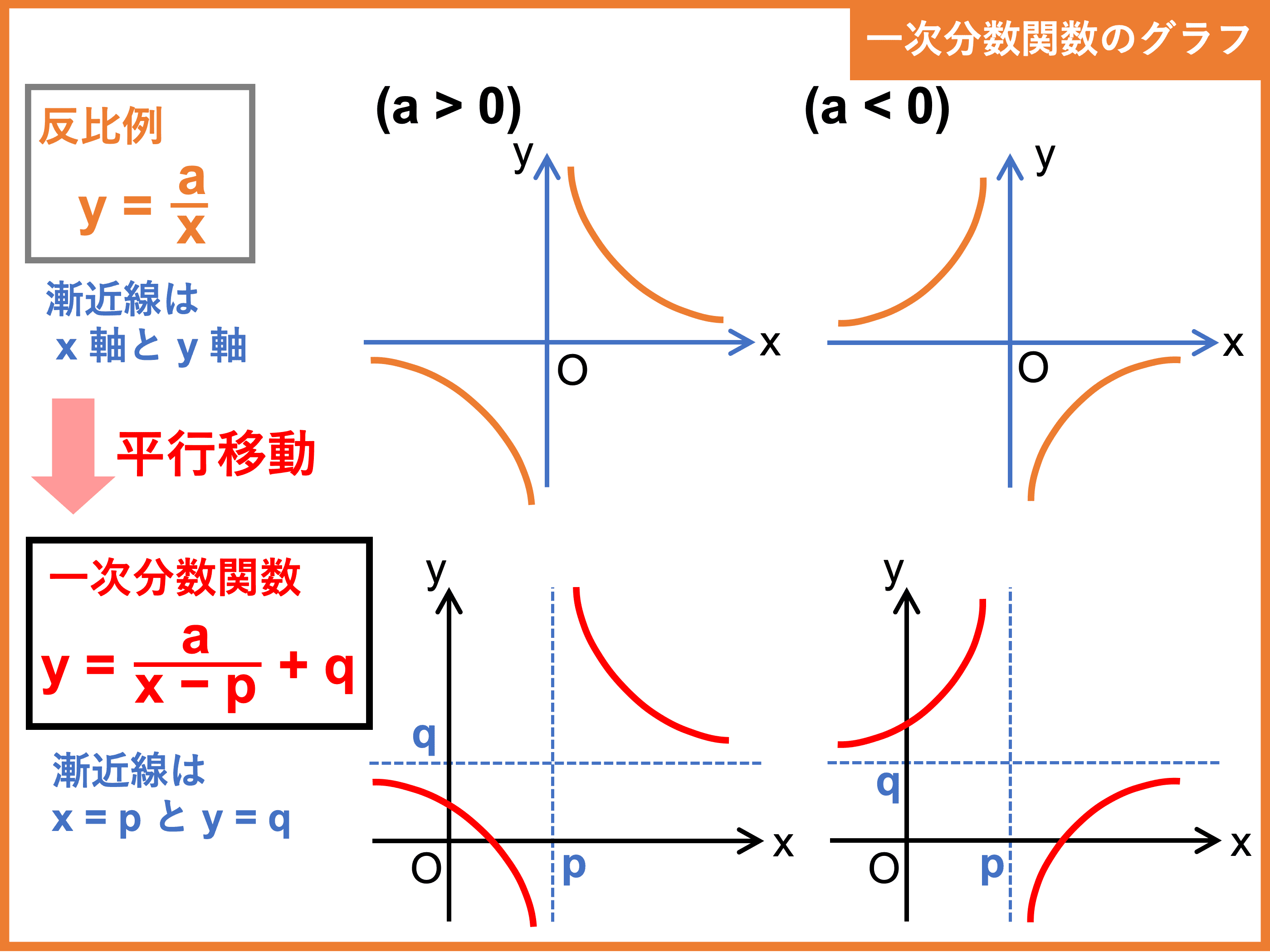


分数関数とは グラフや微分 積分 不等式の解き方 受験辞典



数学 をわかりやすく 頻出問題のひとつ グラフを書け の攻略 Study Supporter
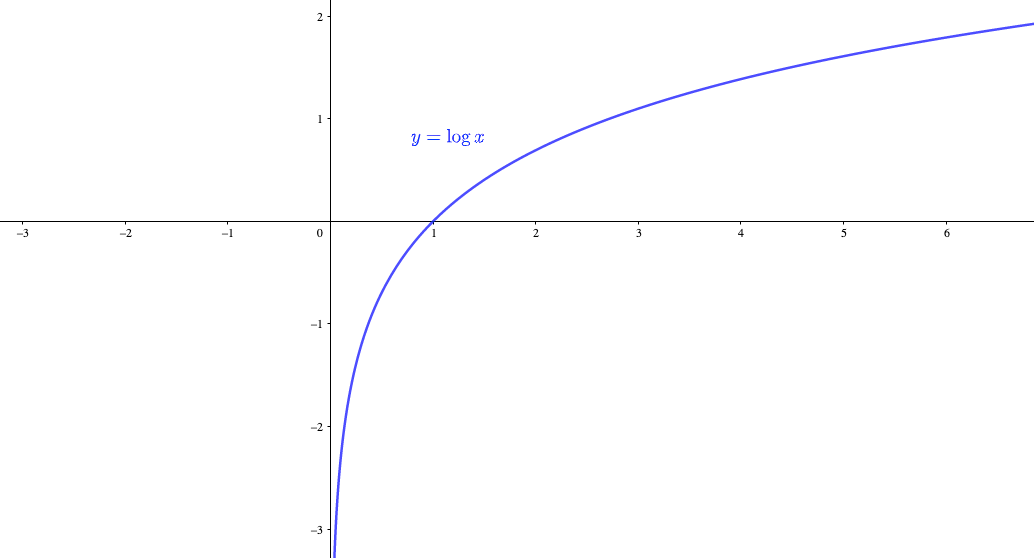


漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック


漸近線の方程式
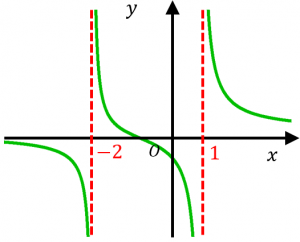


漸近線の求め方3パターン 具体例で学ぶ数学



二つの漸近線から双曲線を求める方法 楕円では 標準形の双曲線の方 数学 教えて Goo



高3 数iiの範囲で図形と方程式 Clear


数3は医学部受験の鍵 勉強の進め方と時期を解説 数3なしの裏技も アガルートメディカル コラム
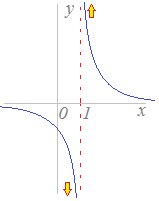


漸近線の方程式
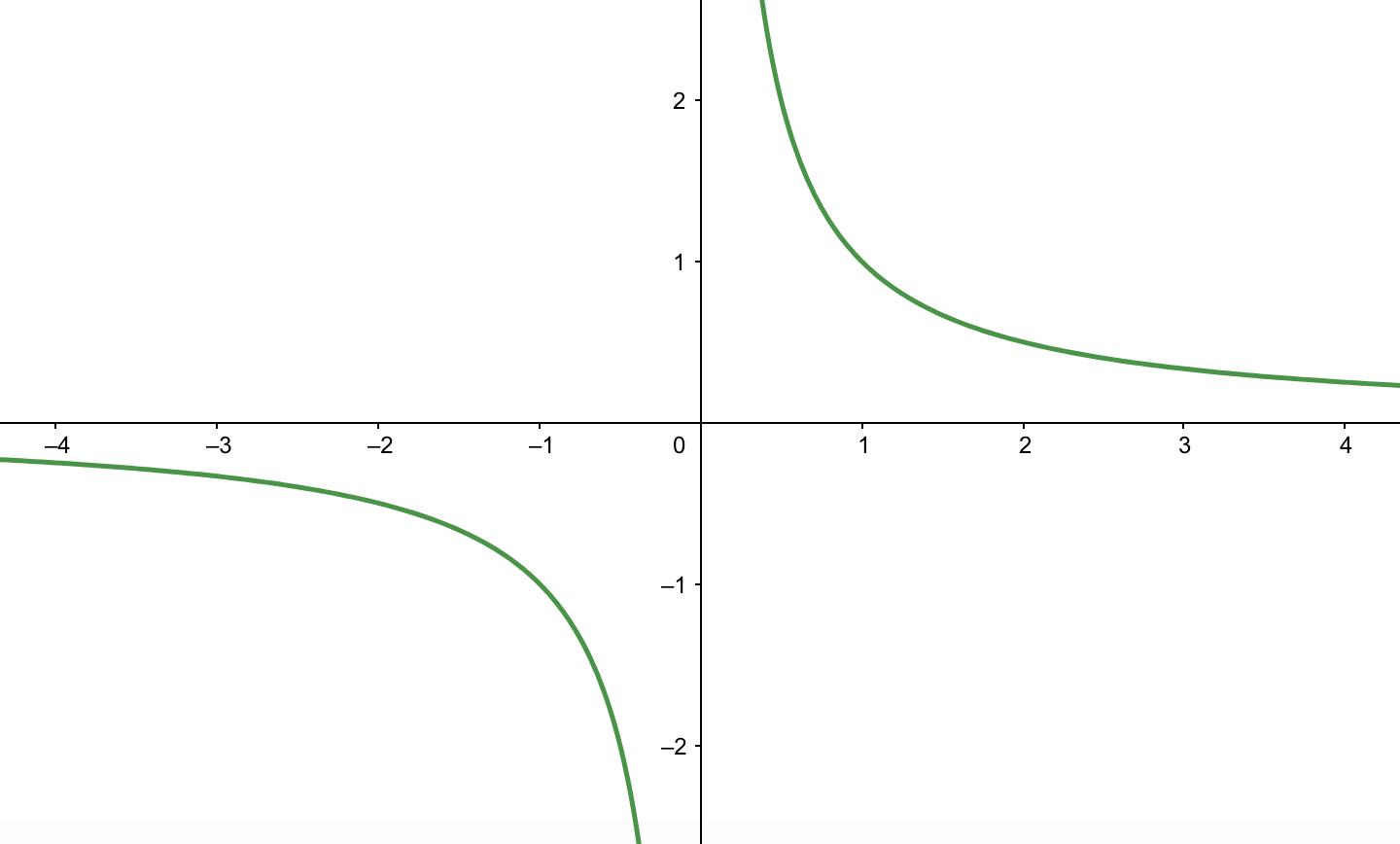


漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック


漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック


基礎数学 2回目


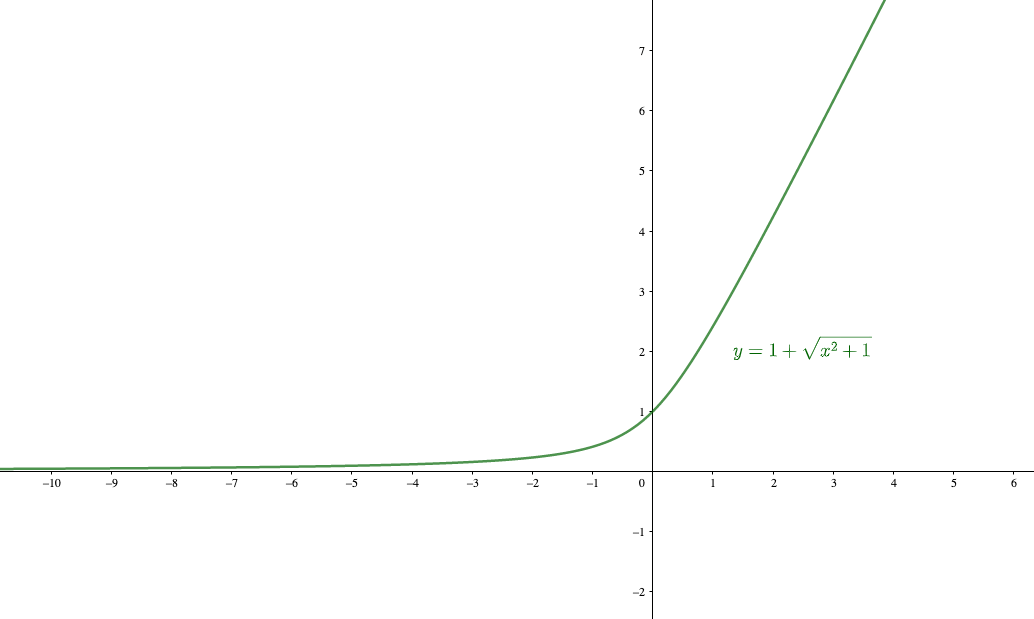
漸近線の求め方3パターン 具体例で学ぶ数学



漸近線の求め方が分かりません 3 です Clear



3分でわかる 三角関数のグラフの描き方 合格サプリ
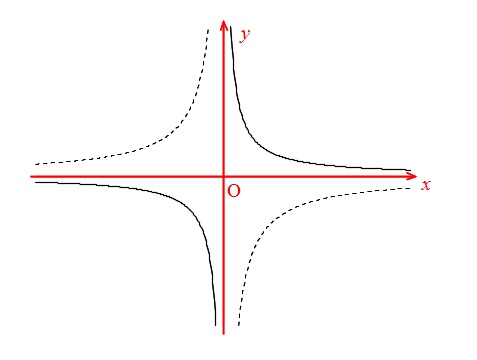


比例と反比例の関数のグラフの形や座標などのまとめ



漸近線の求め方 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc
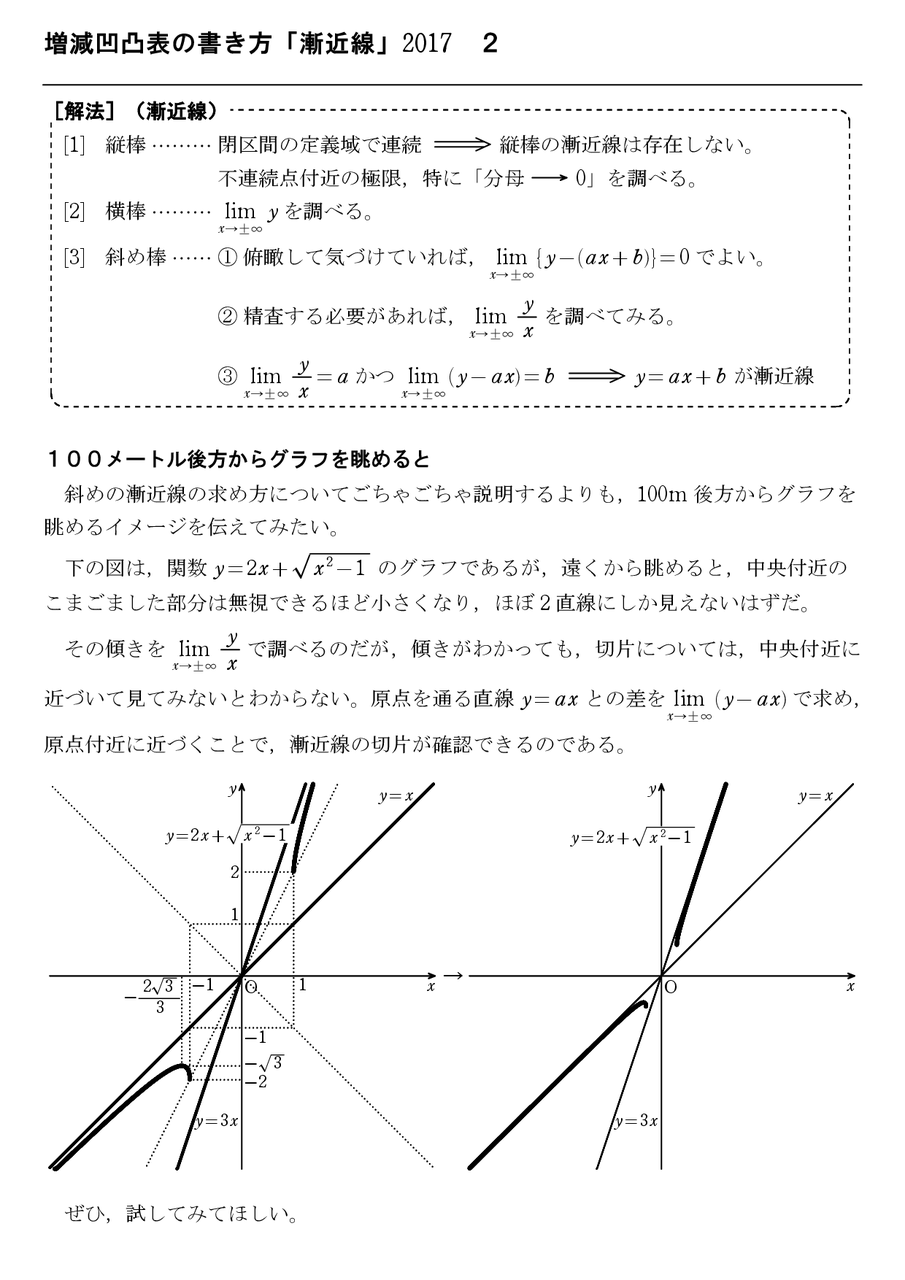


増減凹凸表の書き方 漸近線 17 2 怜悧玲瓏 高校数学を天空から俯瞰する


基礎数学 2回目
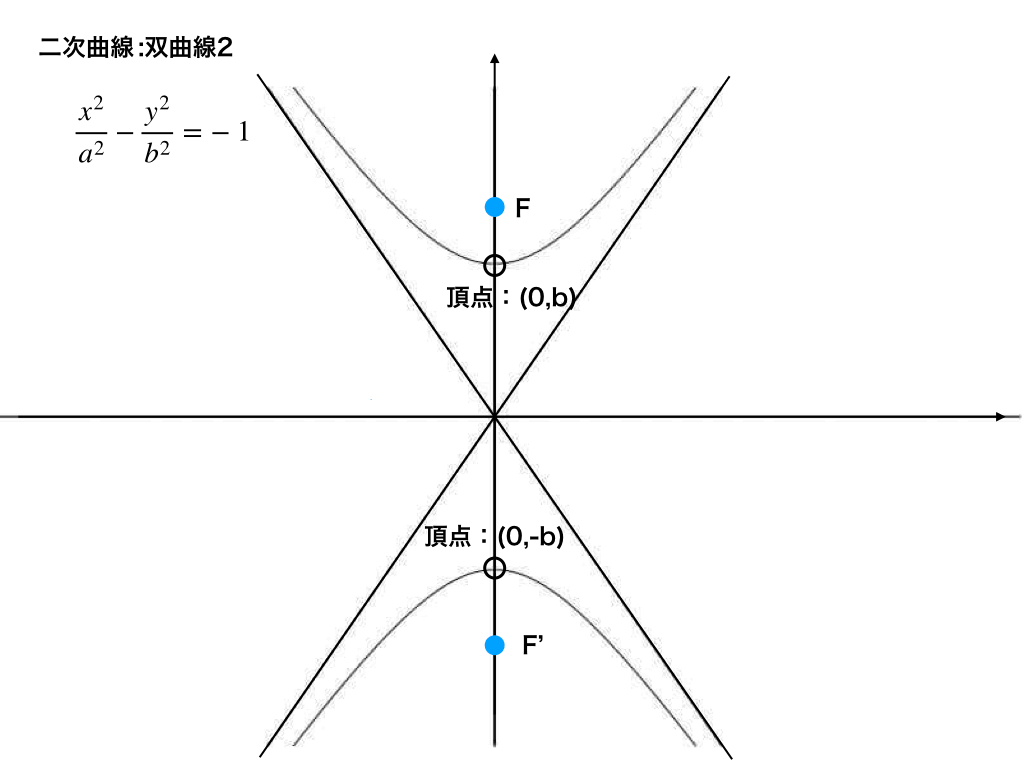


双曲線とは 式の導出とグラフ 漸近線までイラストでわかりやすく解説



極限に関する質問に関する質問 勉強質問サイト



数学 をわかりやすく 頻出問題のひとつ グラフを書け の攻略 Study Supporter
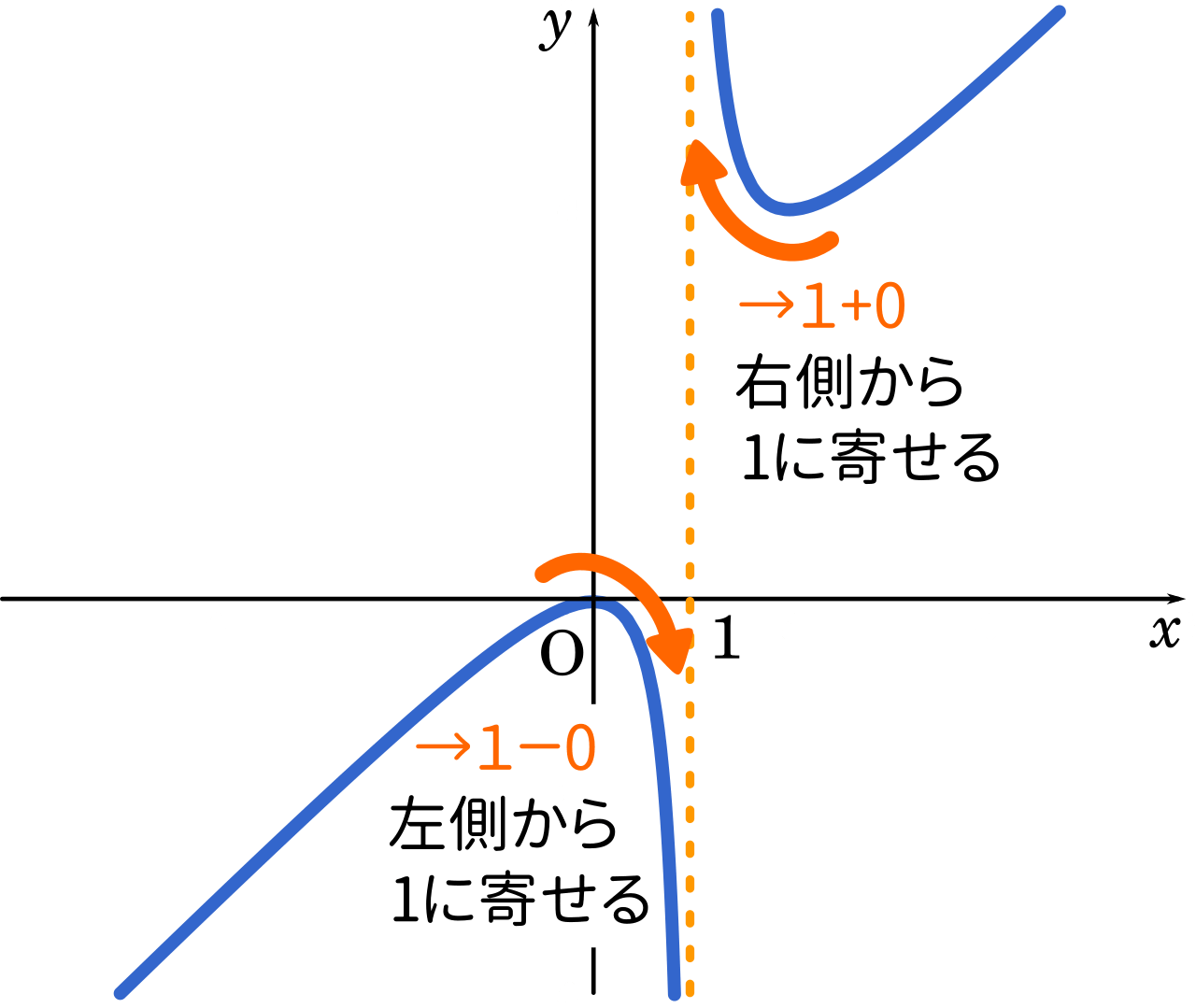


数 微分の応用 ざっくりイメージから漸近線を導く Mm参考書



漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学



高校数学 逆関数の求め方とグラフ 受験の月
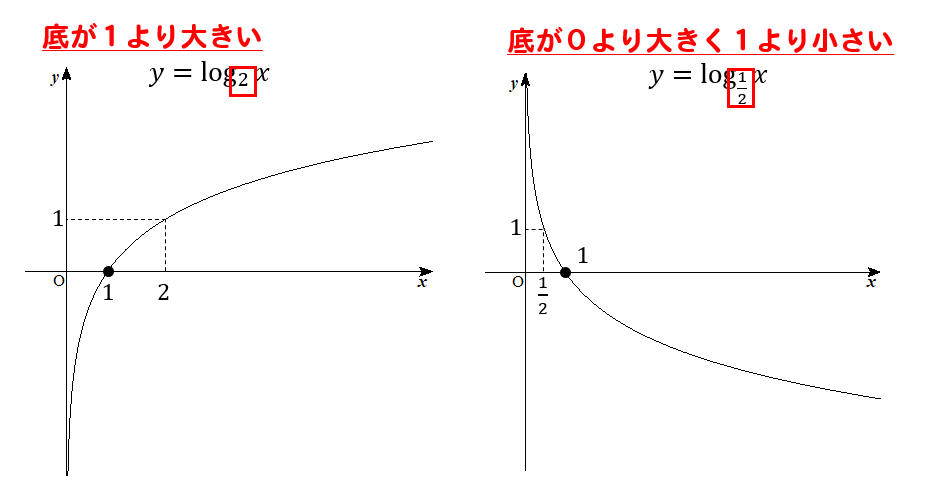


Logのグラフ 書き方を解説 平行移動の場合には 数スタ
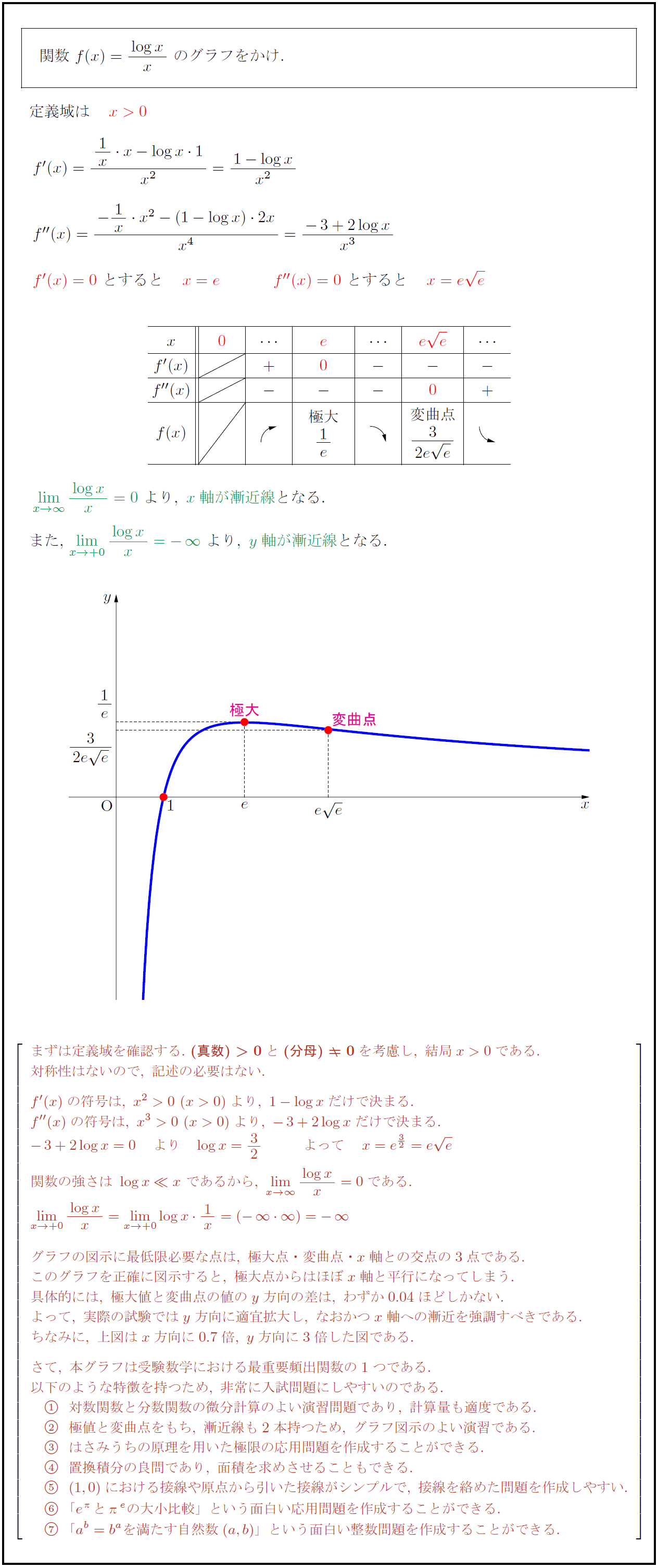


高校数学 対数関数 Y Logx X のグラフ 受験の月


関数y X 2 1 のグラフをかくとき 漸近線の求め方がわ Yahoo 知恵袋
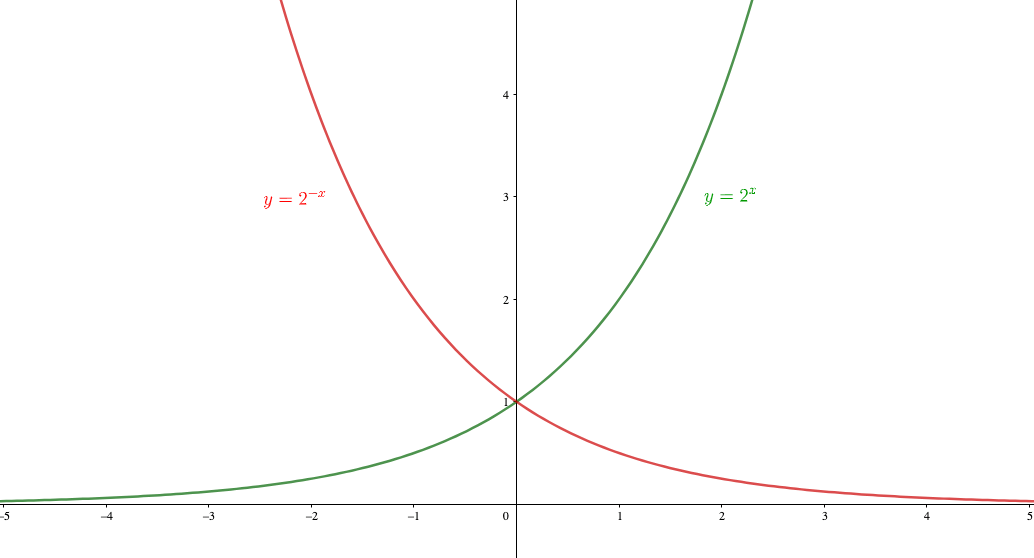


漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック



漸近線の求め方 高校数学 微分法の応用 15 Youtube



漸近線の求め方 高校数学 微分法の応用 14 Youtube


反比例とは グラフの描き方や式の求め方をわかりやすく解説します Studyplus スタディプラス



漸近線を調べて 概形をかけ という問題です 漸近線を求めると 高校数学に関する質問 勉強質問サイト


反比例とは グラフの描き方や式の求め方をわかりやすく解説します Studyplus スタディプラス


漸近展開に関するメモ



漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学
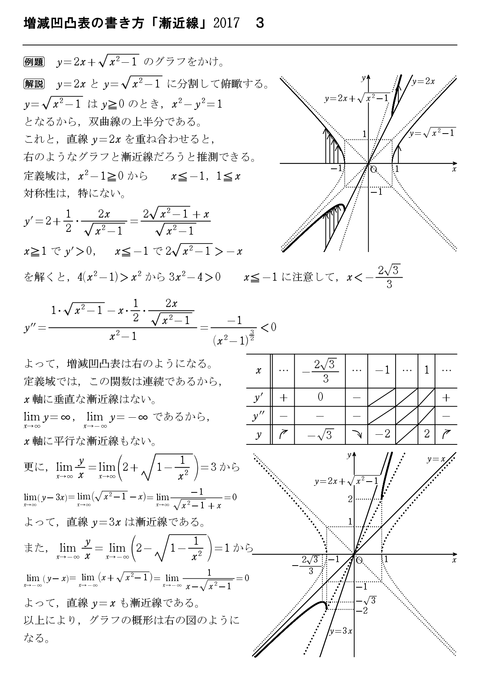


怜悧玲瓏 高校数学を天空から俯瞰する
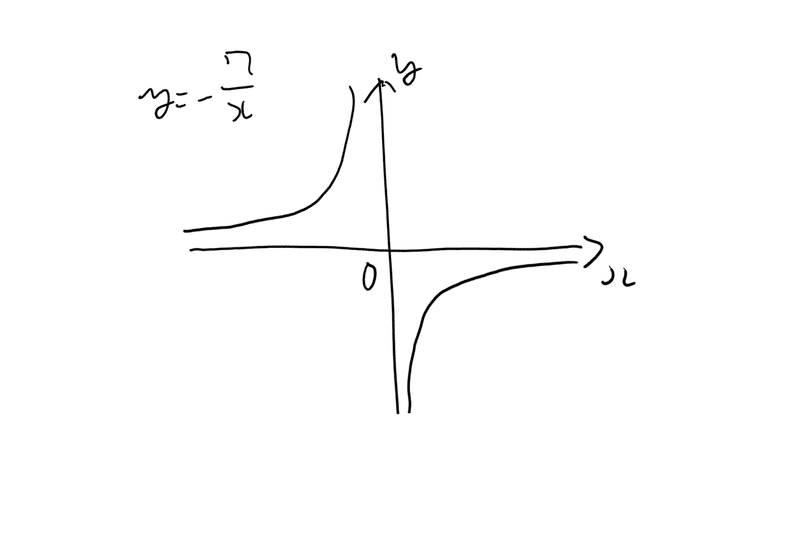


分数関数と無理関数 数 けけどう Note
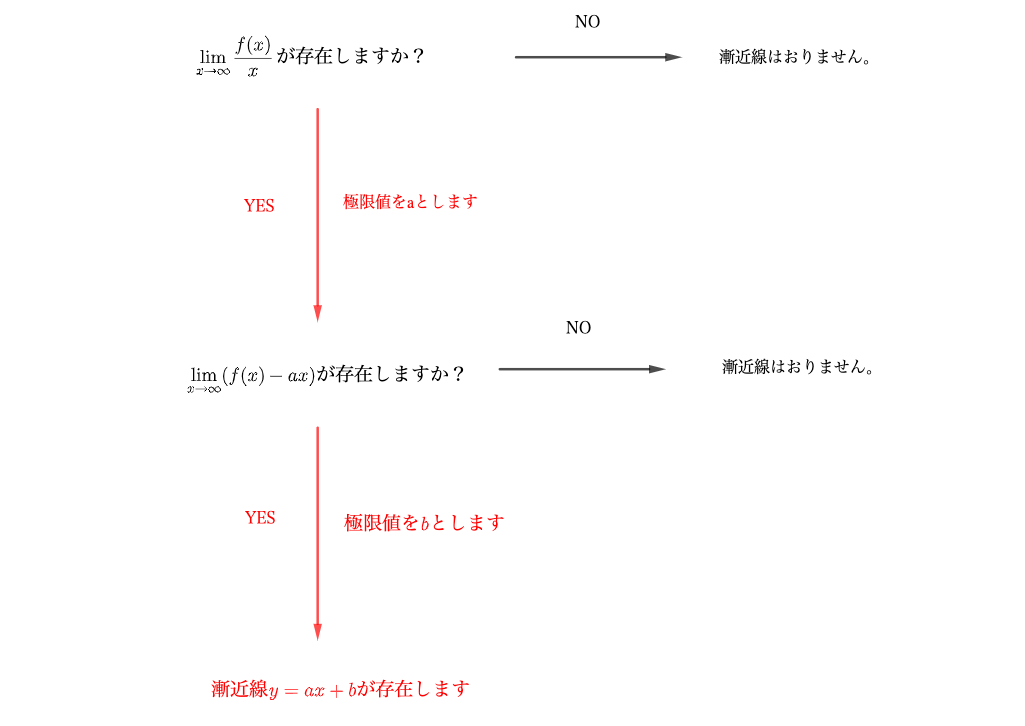


漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック



標準 一次分数関数の逆関数 なかけんの数学ノート



標準 微分と関数のグラフと漸近線 なかけんの数学ノート



漸近線の求め方 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc
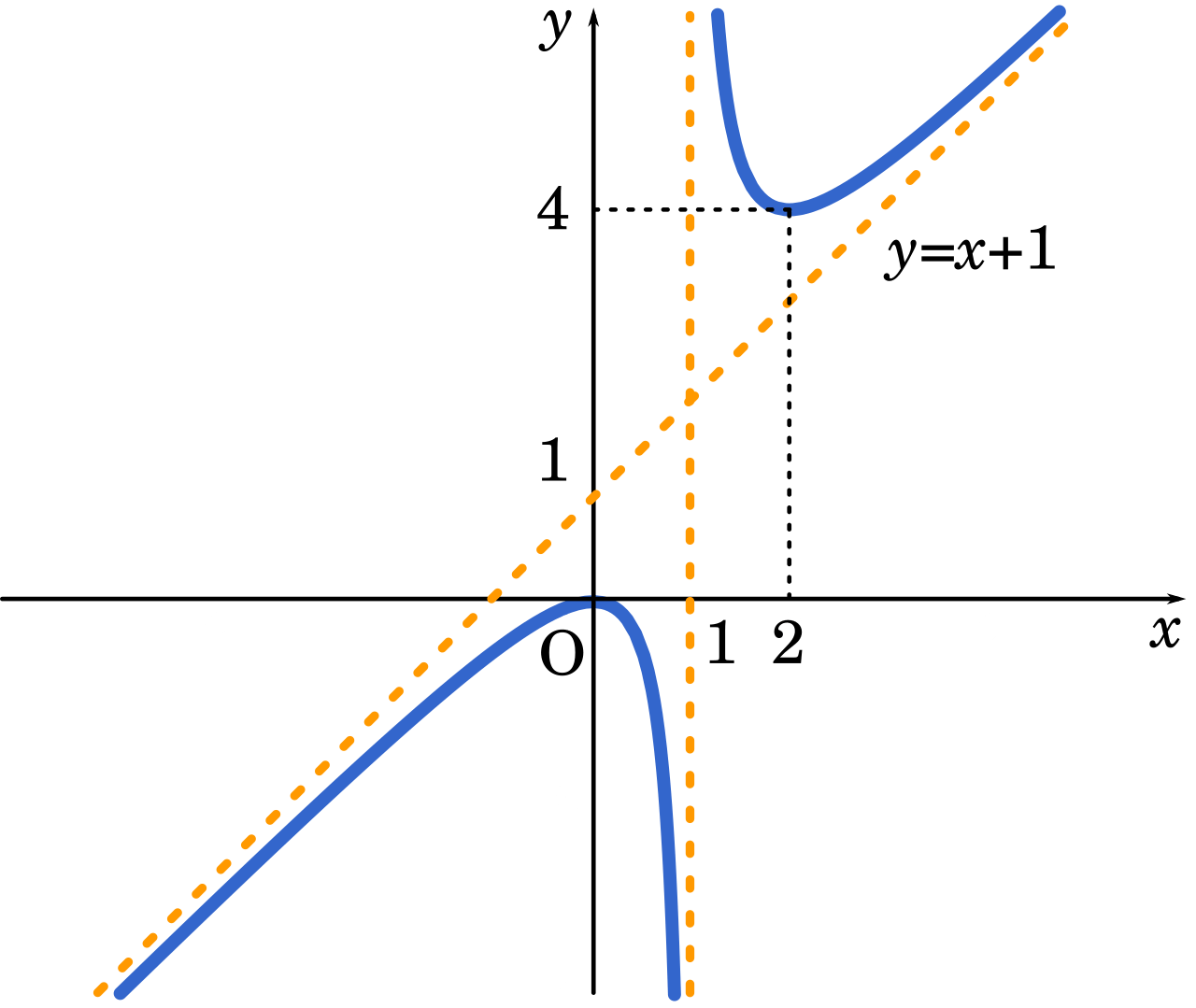


数 微分の応用 ざっくりイメージから漸近線を導く Mm参考書



平成の東大理系数学 1995年 ちょぴん先生の数学部屋
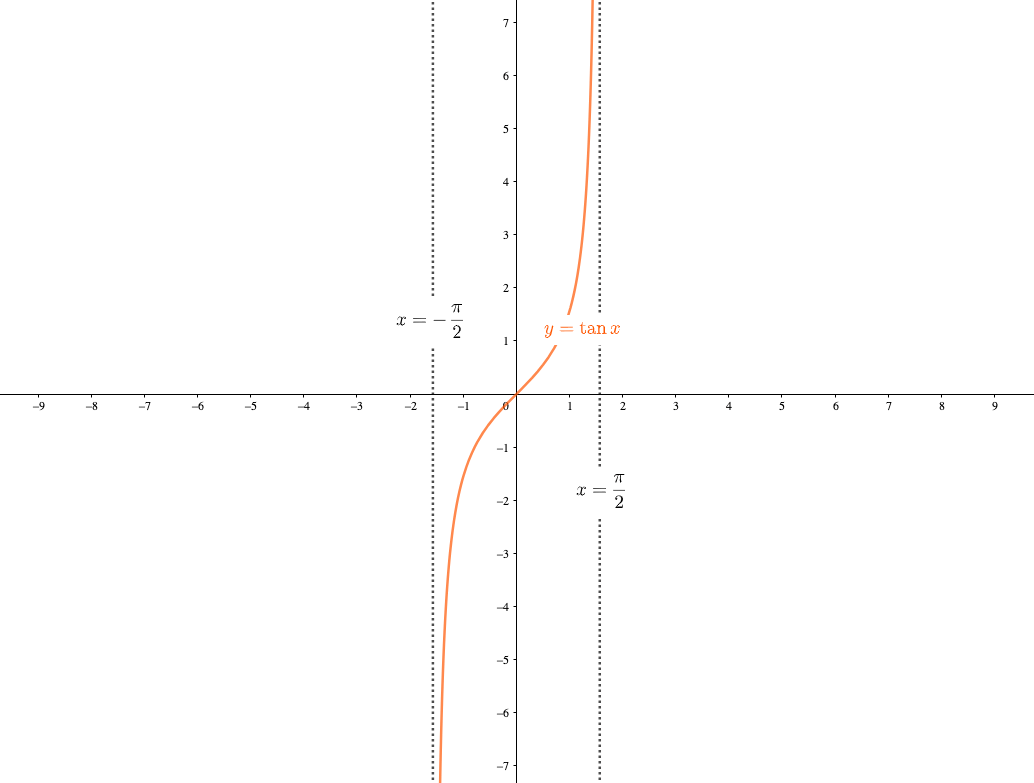


漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック



三角関数のグラフの書き方とコツ Sin Cos Tan 周期 理系ラボ



新入試対応 数学iii基礎問題精講 四訂新装版 上園信武 本 通販 Amazon


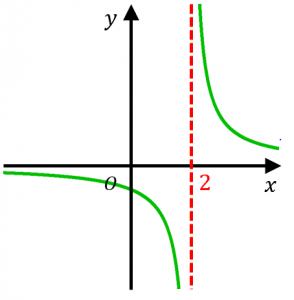
Y 2x 3 X 2の漸近線の求め方を教えてください Y 2x 3 Yahoo 知恵袋



一次分数関数のグラフと漸近線 高校数学の美しい物語
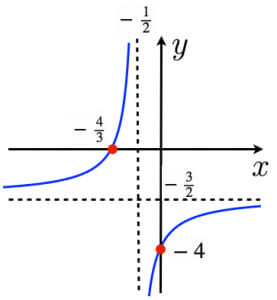


一次分数関数のグラフと漸近線 高校数学の美しい物語



0 件のコメント:
コメントを投稿