· 片対数グラフで傾き A A A ,切片 B B B の直線になる log y = A x B \iff \log y=AxB lo g y = A x B という関係がある y = 1 0 B 1 0 A x \iff y=10^{B}10^{Ax} y = 1 0 B 1 0 A x という関係がある ここで, 1 0 B = C, 1 0 A = a 10^B=C,10^A=a 1 0 B = C, 1 0 A = a とおくと, y = C a x y=Ca^x y = C a x という関係式になる。発展片対数方眼紙で、縦軸に電流、横軸に時刻をとると、 log10I=log10I0-(log10e/RC)t のグラフになる。このグラフの傾き(縦は大きな1マスが1、横軸は普通に読む)=-log10e/RC より、Cを生体では陰性変時作用を心停止の時点まで追跡することは 不可能である。 ※陰性変時作用: 副交感神経が興奮すると心拍リズムが遅くなる こと。

号 腎機能測定のための組成物及びシステム Astamuse
片対数グラフ 傾き 時定数
片対数グラフ 傾き 時定数-片対数グラフの傾きから関数y=Aexp(Bx) の定数A, Bを求める方法 片対数グラフにプロットする事は、方眼グラフでlog 10 yを縦軸にとることに等しい。 したがって対数グラフの書き方 山本昌志⁄ 05年10月4日 1 本日の授業内容 前期の実験で,対数グラフの作成に苦労していた学生が多い.そこで,対数グラフの使い方を説明する.
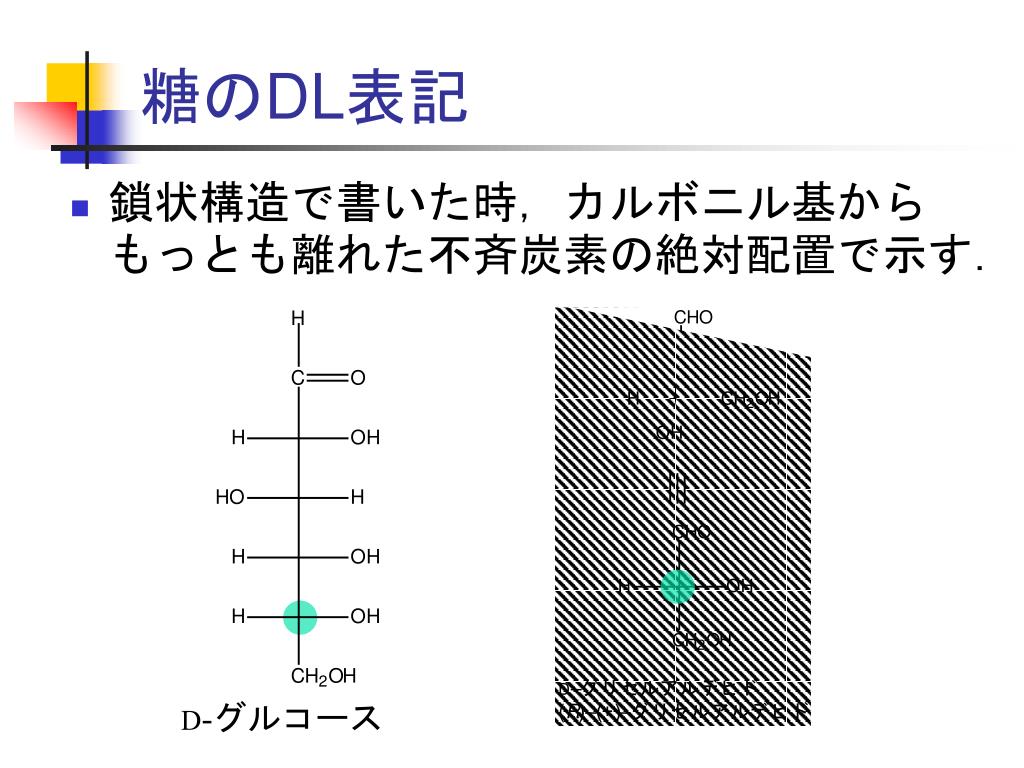



Ppt グルコースの変旋光 Powerpoint Presentation Free Download Id
· ファラデー定数(ファラデーていすう)とは。意味や解説、類語。電子1モルがもつ電気量。記号Fで表し、電気素量eとアボガドロ定数NAの積に等しい。×104クーロン/モル。 goo国語辞書は30万4千件語以上を収録。政治・経済・医学・ITなど、最新用語の追加も定期的に行っています。4 片対数グラフにデータをプロットし、その傾きから 時定数を計算する。ただし、得られたデータをその ままプロットしても、片対数グラフを使う意味がな い。どのようなプロットを行えばよいか、考えるこ と。式(6) がヒントになる。 5 得られたデータを対数プロットして充電時の時定数 を求めよ。 · ここで、この回路の時定数は、eの累乗部分の係数R/Lの逆数である \\tau=\frac{L}{R}\ となります。 これが、時定数の公式です。 つまり、過渡解がe^atのとき、時定数はτ=1/aとなります。 次は公式を用いずに求めてみましょう。
数k との間に片対数グラフ上で直線関係が認められた1)。 BDerby とMFAshby はn と他の実験定数との間に片対 数グラフ上での直線関係を指摘している2)。本研究は,応 力指数n と係数k の関係式k = BAn(A,B実験定数) がク片対数グラフとは、「x軸: 普通の目盛 、y軸: 対数目盛 」や「x軸: 対数目盛 、y軸: 普通の目盛 」のようにx軸またはy軸の 片方 が対数目盛となっているグラフのことを指します。 片対数グラフは英語では「SemiLog Plot」または「SemiLog Graph」と書きます。 両対数グラフとは、「x軸: 対数目盛 、y軸: 対数目盛 」のようにx軸とy軸の 両方 が対数目盛となっている対数増殖と呼ぶ。図1は 対数増殖にあるバクテ リアの増殖を片対数紙と普通グラフ用紙で示し たものである。 図1 世代時間td=1hrの バクテリアの増殖曲線 左片 対数グラフ 右普 通のグラフ用紙に書いたもの 微生物の増殖の速さを比較するにはμの大
· 片対数グラフ:縦軸を対数にするだけで直線になる 「縦軸を対数にするだけで直線になるような関係性がx x とy y にあった」 というのがポイントになるわけです。 そのような関係性にあるものは何かというと 指数関数 です。 例えば、下記のような関係式が成立しているような場合などが当てはまります。 y = ae−bx (1) (1) y = a e − b x これが上図の左の関係①上の表のグラフを片対数グラフ用紙に折れ線グラフ で書く。 ②y=2 x と同じ傾きのグラフをその上に書く。 つまり、142万台(1945年)から順調に5年おきに2倍に (1950年142×2=284万台 · 片対数グラフと傾き・切片の出し方 大学の物理実験の前に、準備としてグラフの書き方を教わっています。 そこでの練習問題なんですが、V=V0e^αtという式があり、いくつかの数値と計測回数が書いてありま
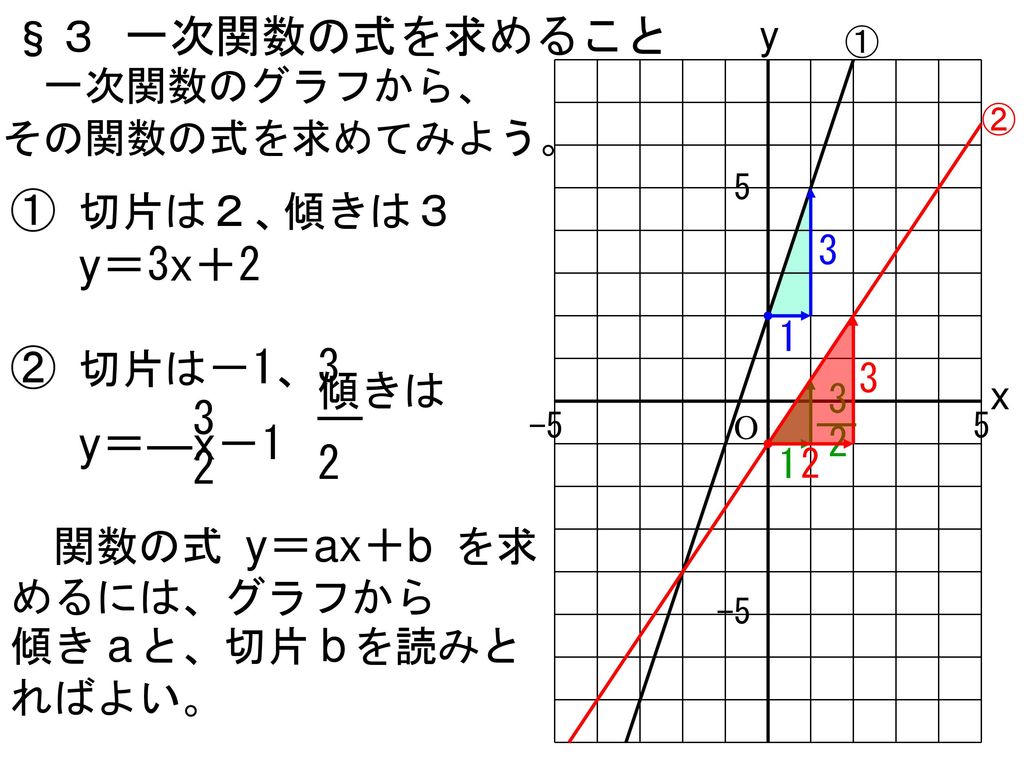



エクセル 一次 関数 グラフ
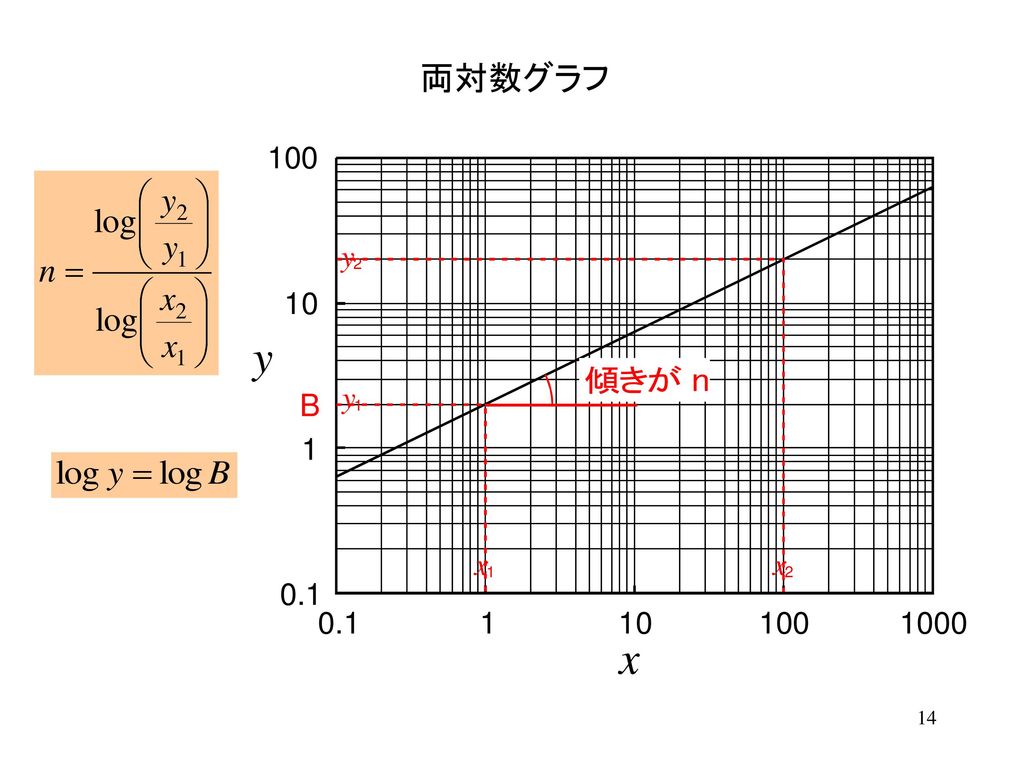



電気基礎実験 グラフ処理 Ppt Download
· rc直列回路の時定数について 先日学生実験を行ったのですが、片対数用紙で作成したグラフの傾きから時 定数 CRの値を求める問題が解けません。 最小二乗法を用いてグラフの傾きを求めて、そこから計算してみたのです片対数グラフ(かたたいすうぐらふ、semilog graph) とは、グラフの一方の軸が対数スケール(縦を対数スケールとすることが多い)になっているグラフである。 極端に範囲の広いデータを扱える。通常の目盛(線形スケール)の軸を範囲の狭いデータに、対数スケールの軸は極端に範囲の広い · この式の定数「T」が「時定数」です。 「傾き」ではなく、上記の特性式にフィッティングして、「T」の値を求めてください。 ①であれば、両辺の自然対数をとった式 ln(y) = ln(A) t/T




号 腎機能測定のための組成物及びシステム Astamuse




Ppt グルコースの変旋光 Powerpoint Presentation Free Download Id
紙である。図3 の左は縦軸が対数目盛であ る片対数方眼紙,右図は縦軸,横軸がとも に対数目盛である両対数方眼紙である。 まり,片対数方眼紙に指数関数のグラフを 描くと,傾き 直線のグラフとなる 図 3 :対数方眼紙 (菅原正巳, 1951 ,p254) · このデータに対し、最小2乗法を適用すると、 Y = 1500 X 5966 × 10 − 5 = a X b となります。 この a = 1500, b = 5966 × 10 − 5 を変換後の式 y = b ′ x a ( b ′ = 10 b) に代入してあげましょう。 すると、 y = 10 5966 × 10 − 5 x 1500 = 1000 x 1500 という関係式が成立します。 つまり、公転周期は軌道半径の15乗になるということがわかりますね。 少し言い換えると、公転0621 · 発条定数(ばねていすう)とは。意味や解説、類語。ばねが受けた荷重と伸びとの比。ばねの弾性定数。 goo国語辞書は30万4千件語以上を収録。政治・経済・医学・ITなど、最新用語の追加も定期的に行っています。
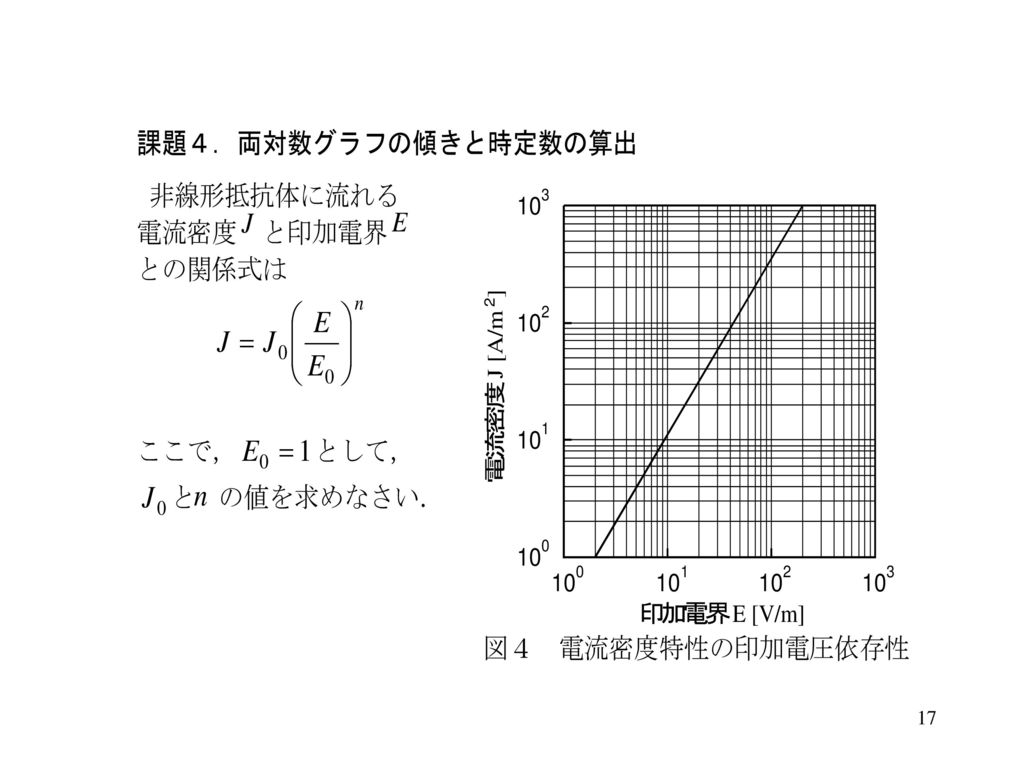



電気基礎実験 グラフ処理 Ppt Download




Jpa 少なくとも1つの保護されたチオール領域を有するアルブミンベースコロイド組成物 その製造方法および使用方法 Google Patents
図8 片対数グラフ べき関数の式(3) を変形する。y = 10Y を代入し、両辺の10 の対数を取る。 y = 08x2 10Y = 08x2 Y = 2log 10 jxjlog 10 08 Y ≃ 2log 10 jxj Y とx は対数関数となり、図8 のべき関数を表す赤線は線形線形グラフ(図7)の対数関数(緑線)と近い上に 凸の曲線になっている。この時、測定した電圧を対数軸に、時間 を線形軸にプロットする。放電の片対数グラフで測定点を通る直線を引いて時定数を求めよう。 レポートでは以下の点について考察せよ。 片対数グラフで直線を引いて時定数を求めることができる。これは何故か?この振幅比の自然対数をとったものが対数減衰率と言いδとすると、式21、22 より 2 2 1 1 2 ζ πζ δ ζω0 − = = T = a a "n 式23) ζ≪1 なら δ=2πζ (式24) と減衰比に2πをかけた値になる。 ② ζ=1 のとき この時は C =Cc の時の現象で、 この状態を臨海減衰と言い
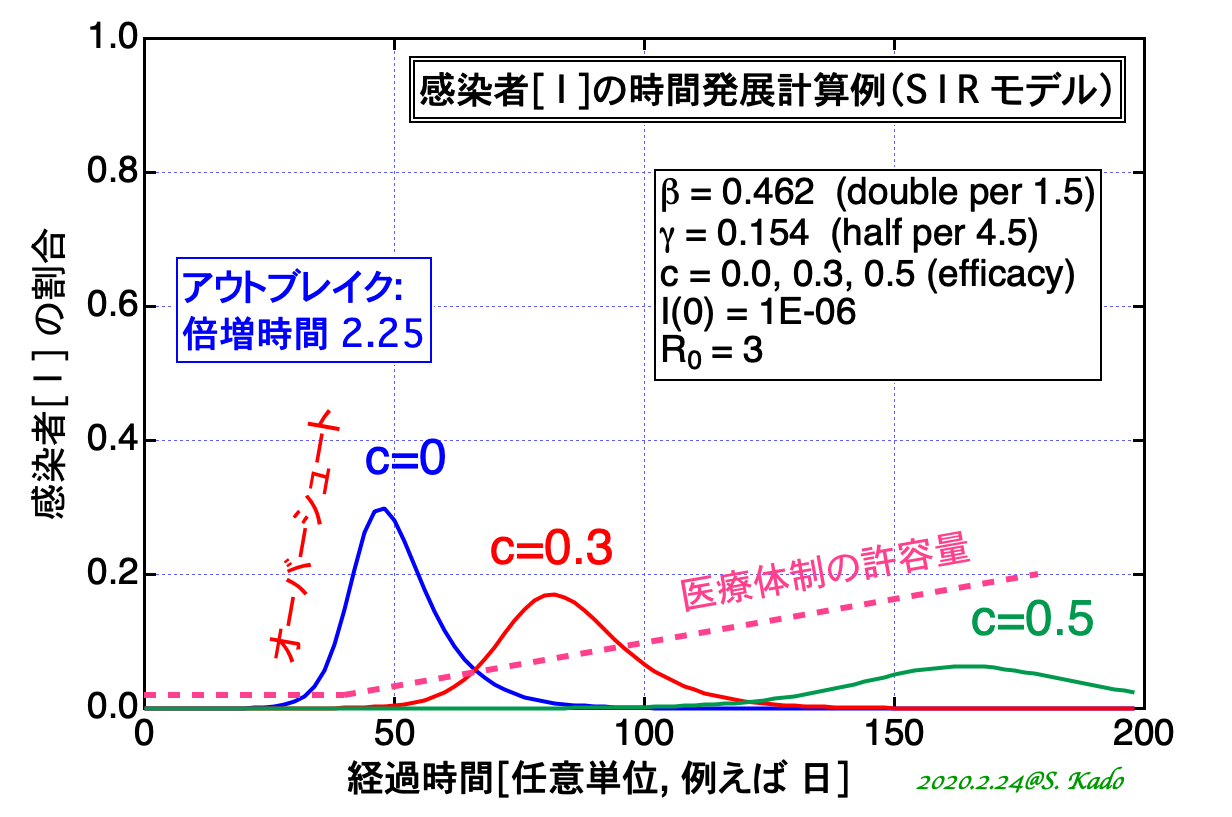



この感染は拡大か収束か 再生産数 R の物理的意味と決定 単純なモデル方程式に基づく行動変容の判断のために Rad It21



緩和現象 けての物理 Rtmよも急発信所
· 手順2 傾きと切片を求める 片対数グラフでは,y座標の間隔が調整されているだけで値は変わってません.そのため,このまま直線の傾きを求めようとしても,傾き一定に 見えている だけなので増加率は場所によって異なってきます. ではどうするかというと,グラフから読み取れる2つの座標 ( x 1, y 1), ( x 2, y 2) のうち,y座標に常用対数 log 10 をとった上で · タイトルの内容について質問です。 生物薬剤学の教科書で静脈内投与の場合の線形1コンパートメントモデルにおける薬物の血漿中からの消失のグラフが2種類ありました。 普通軸のものと時間に対して血漿中薬物濃時 定数 片 対数 グラフ 5 1511 Written by ぷよぷよ 二次創作 ガイドライン 5, Solidworks Api Part 6, カーコンビニ倶楽部 全塗装 料金 7, 今宵こそ パック 値段 24, 水切り ヨーグルト バスク チーズケーキ 生クリーム なし 11, バイト シフト 減ら され た コロナ 7,



スライド 1



Ct4lveexrnpdtm
· 時定数の求め方について質問です。 コンデンサの電圧をVcとしたとき、正弦波交流波形において Vc=V×e^(t/RC) となると思うのですが、これを片対数グラフにプロットして傾きから時定数を求めたいです。 · 左辺は反応速度の濃度依存性を除いた反応速度定数で、濃度一定の時 OKなら傾き から活性化 市販されている「片対数グラフ用紙」ではの用紙を縦につかうもので横軸には1mmが一目盛りで180目盛りを、縦軸には常用対数で4サイクル( · RC(アールシー)とは。意味や解説、類語。《reinforced concrete》鉄筋コンクリート。 goo国語辞書は30万4千件語以上を収録。政治・経済・医学・ITなど、最新用語の追加も定期的に行っています。



Ew 基礎薬学完成 Egword




力学 減衰振動 2階斉次線形微分方程式の解法をわかりやすく解説する 宇宙に入ったカマキリ
対数目盛について 対数の値は、log1=0、log2=、log3=、log5=、log10=1、log100=log10 2 =2log10=2、log1000=log10 3 =3であるので、対数目盛と実際の長さは図のようになっている。 従って、対数目盛の数値のところに点を取れば、常用対数の値になっている。 下の図では、対数 log 10 = 1を長さ100mmにNext 23 詳細な性質 Up 2 なぜ対数グラフを使うのか Previous 214 対数対数 両対数グラフ 22 それぞれのグラフの性質 どの関数がどのグラフで直線で描かれたか表1に纏める。 関係のわからないあるデータが得られた時に、普通のグラフに描き直線状に分布すれば線形関数( )であることが分かる。



Dwhemevoh6uwkm
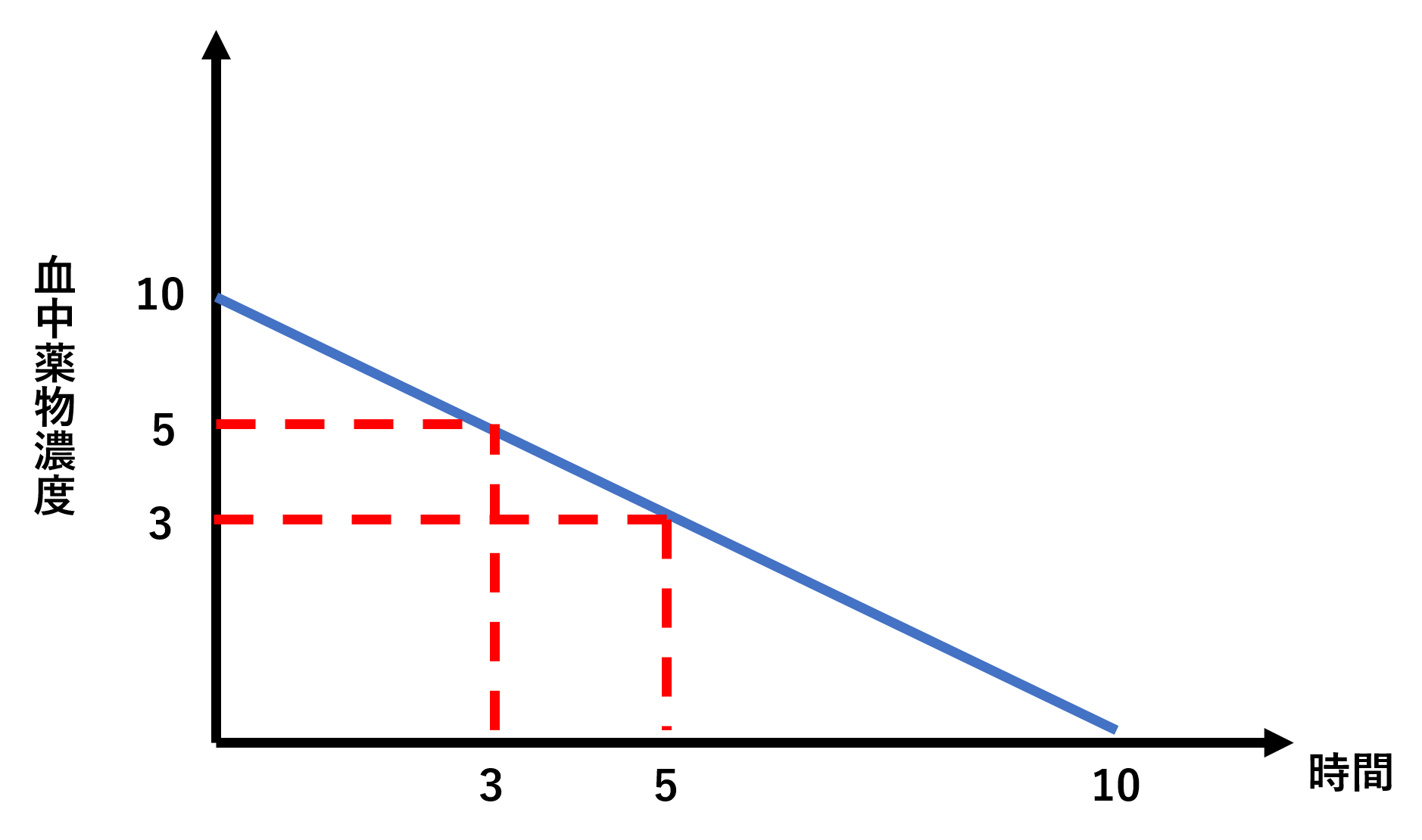



薬物動態 消失半減期t1 2とグラフの読み方
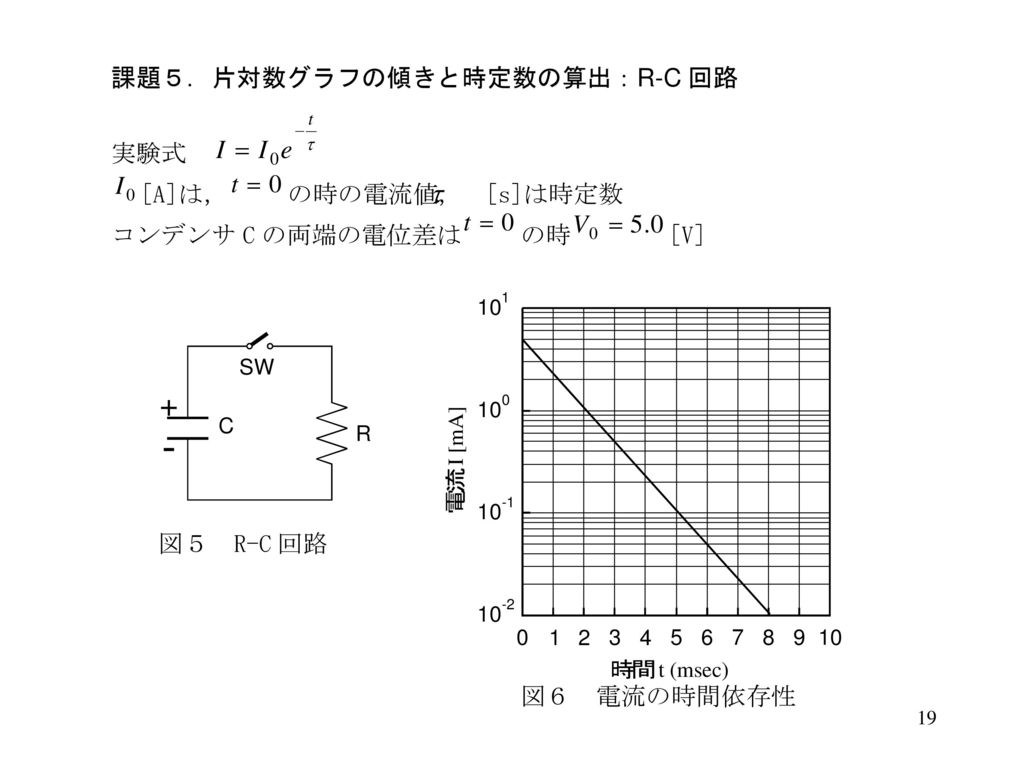



電気基礎実験 グラフ処理 Ppt Download




傾き 微分 を求めたい 添付写真の三角波の傾き Dvi Dt をグラフか Okwave
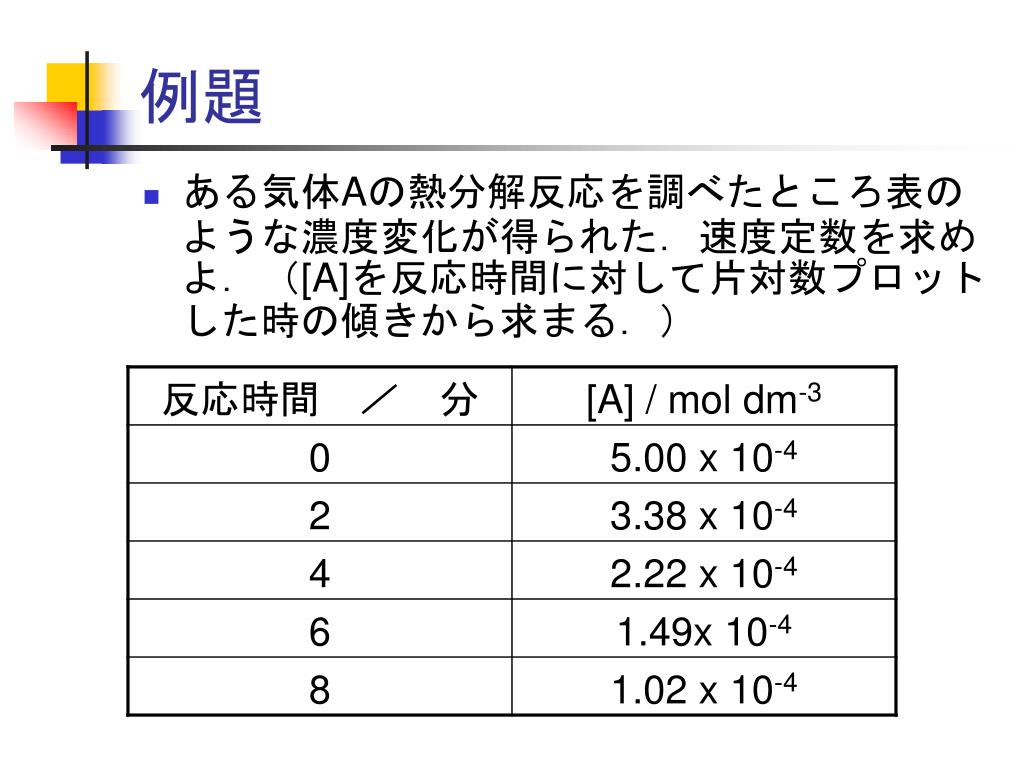



Ppt グルコースの変旋光 Powerpoint Presentation Free Download Id
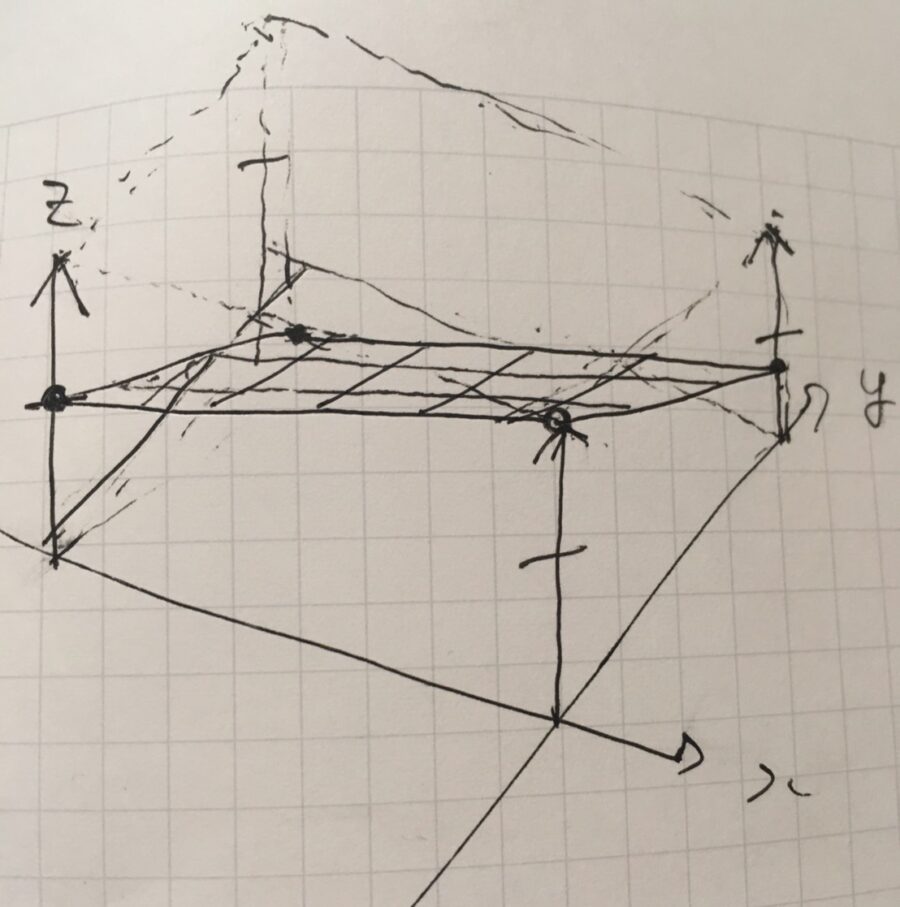



グラフ 勾配 意味
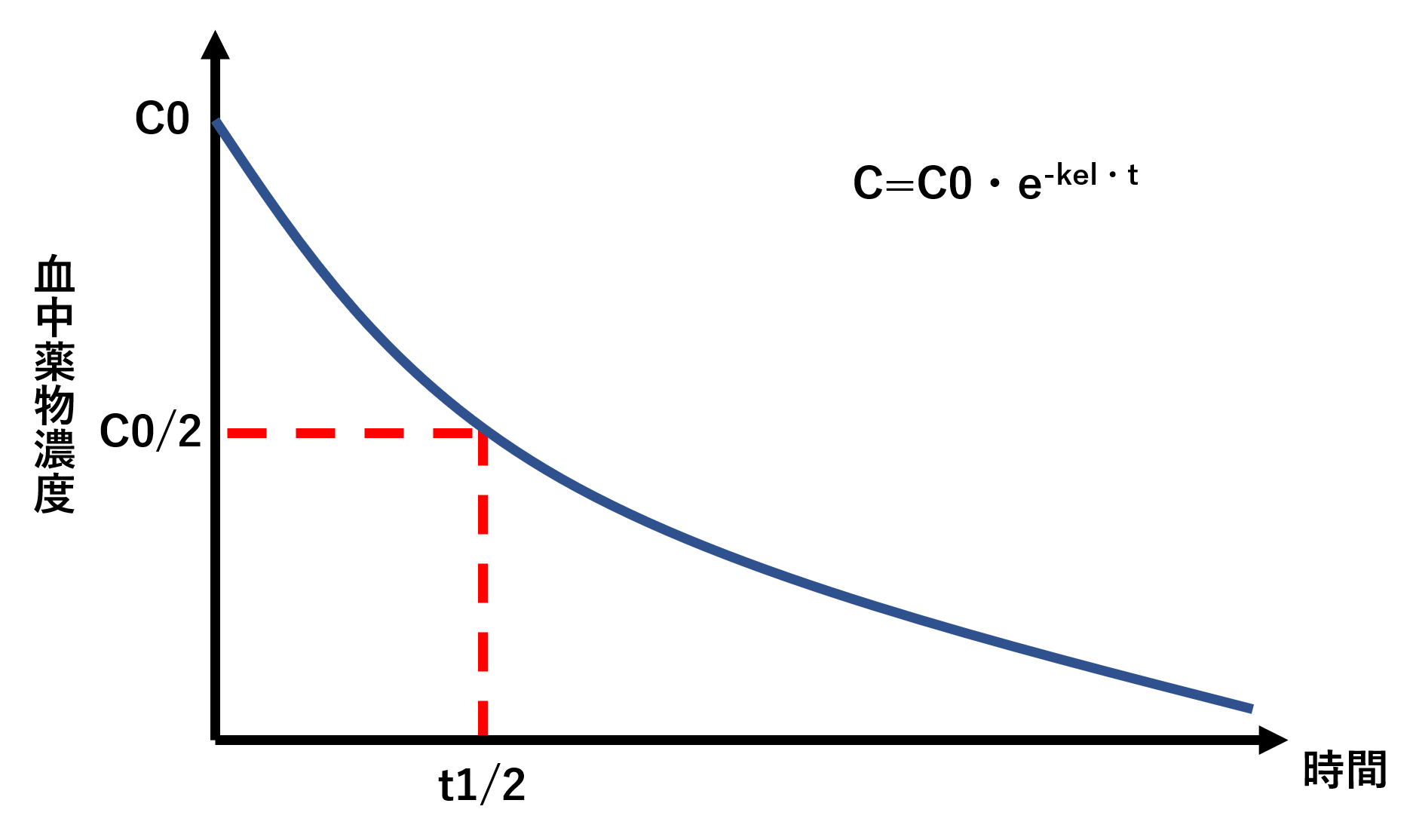



薬物動態 消失半減期t1 2とグラフの読み方




アレニウス プロット 傾き 活性化エネルギー e と頻度因子 A について先週反応速度の実験を行いまし



公開特許公報




Jpa ox40l融合タンパク質およびその使用 Google Patents




シグモイド関数 Wikipedia
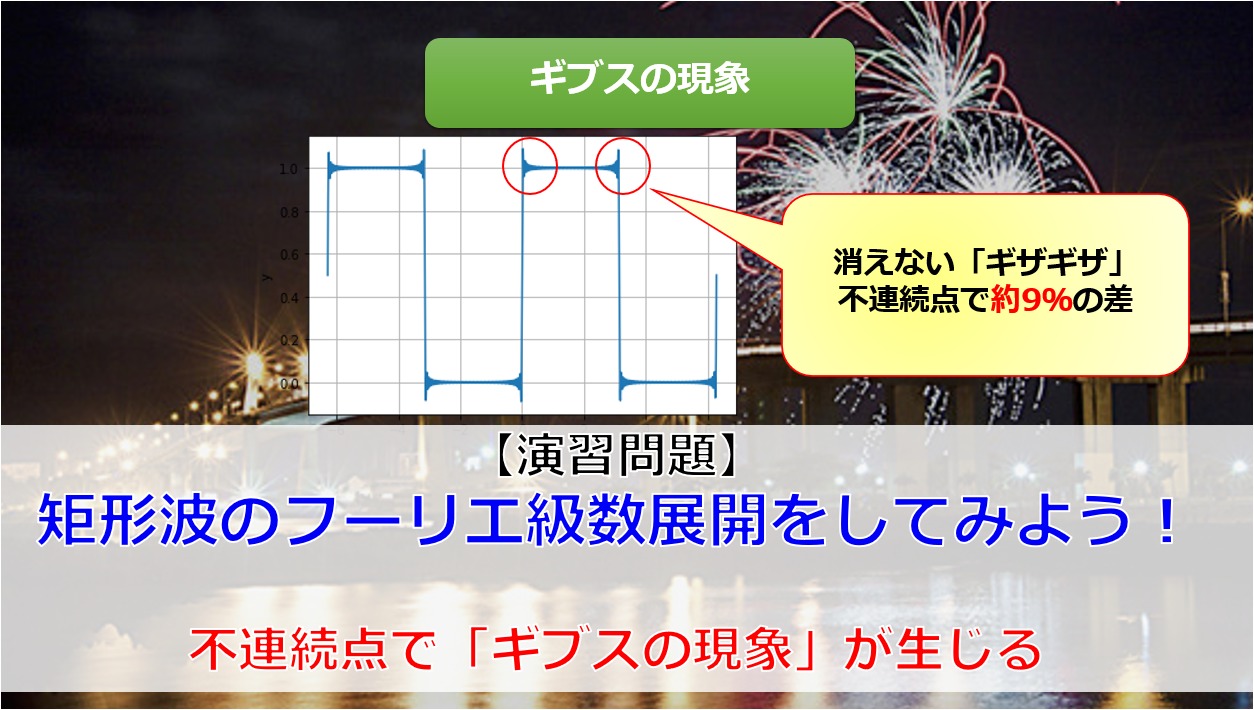



高校生からわかる片対数グラフと両対数グラフを使うと直線になる理由 宇宙に入ったカマキリ




ポイントは入力セトリング時間の最適化




バトラー ボルマー式 Wikipedia
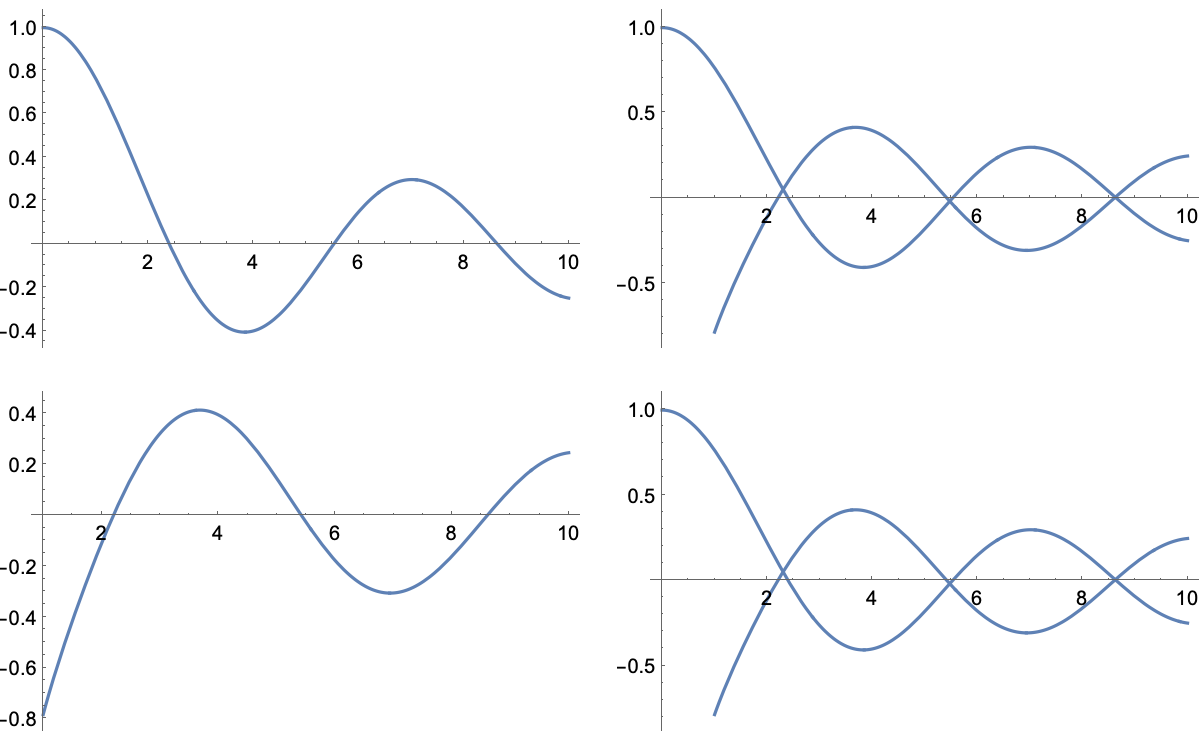



グラフィックスとサウンド Wolfram言語ドキュメント




号 腎機能測定のための組成物及びシステム Astamuse




11 号 乗法九九学習具 Astamuse




Jpa ox40l融合タンパク質およびその使用 Google Patents




エクセル 一次 関数 グラフ



Ew 基礎薬学完成 Egword




薬物動態 消失半減期t1 2とグラフの読み方



ある薬物300mgをヒトに静脈内投与したところ 下の片対数グ Yahoo 知恵袋



片対数グラフとは何か Training Day



7 1 そもそもa Ab B級動作とはアイドリング電流や動作時の電流変化により分けられます C級動作なんて動作条件もありますが C級動作は高周波の世界の話でありオーディオアンプでは使いません 近年では何故かd級アンプなんて物もあります



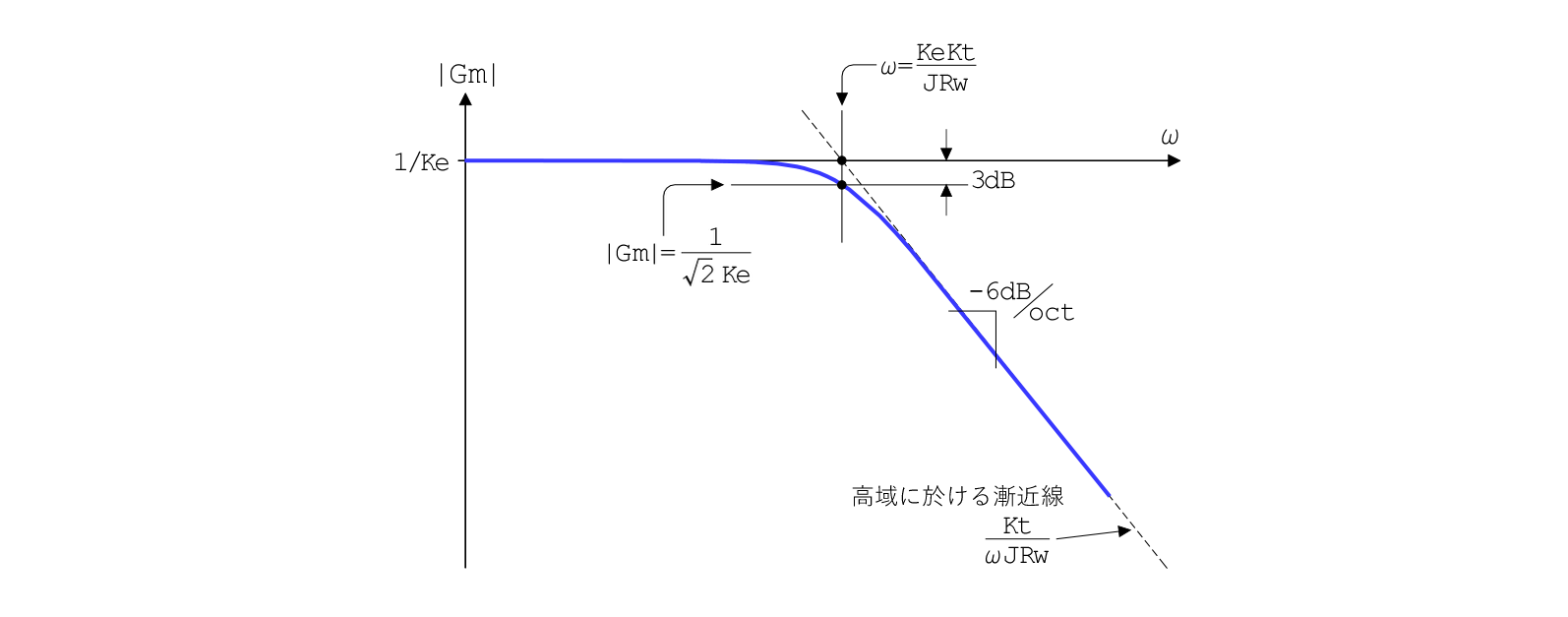
ボード線図
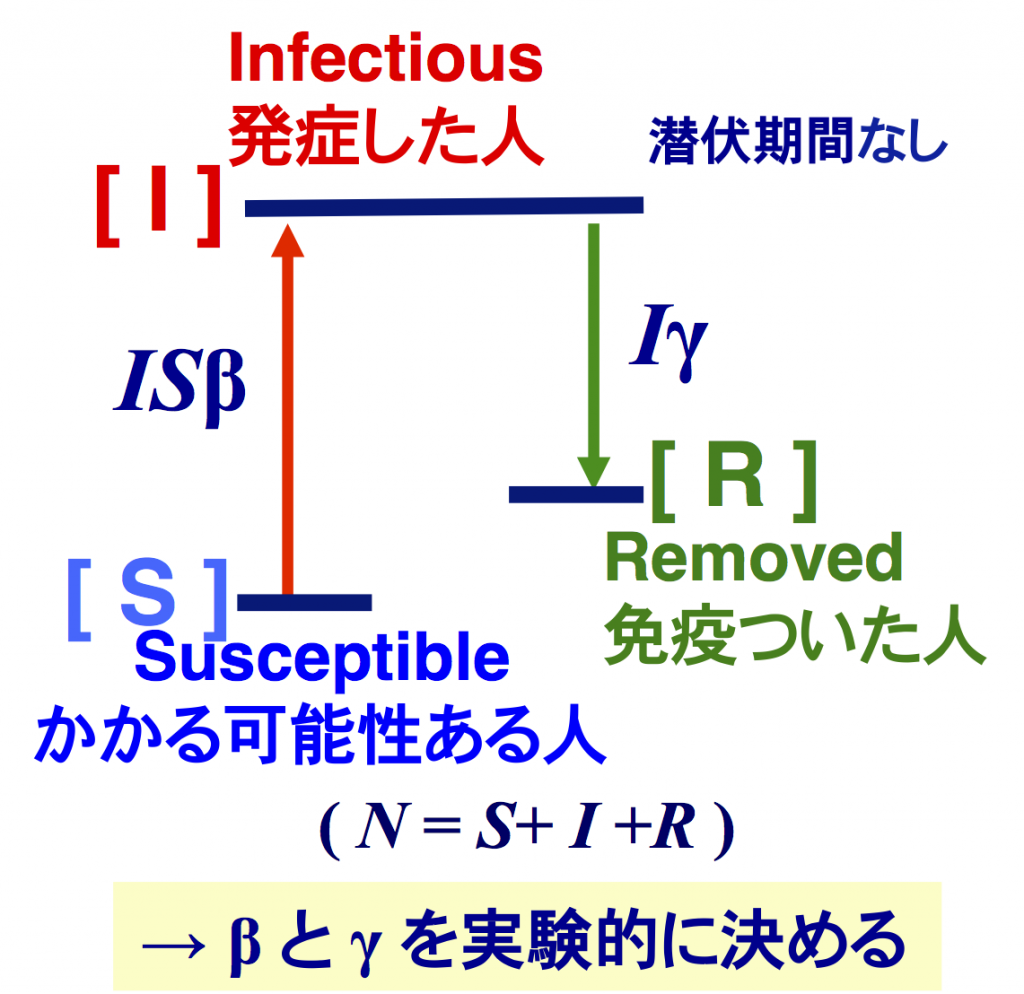



この感染は拡大か収束か 再生産数 R の物理的意味と決定 単純なモデル方程式に基づく行動変容の判断のために Rad It21




片対数グラフとは何か Training Day
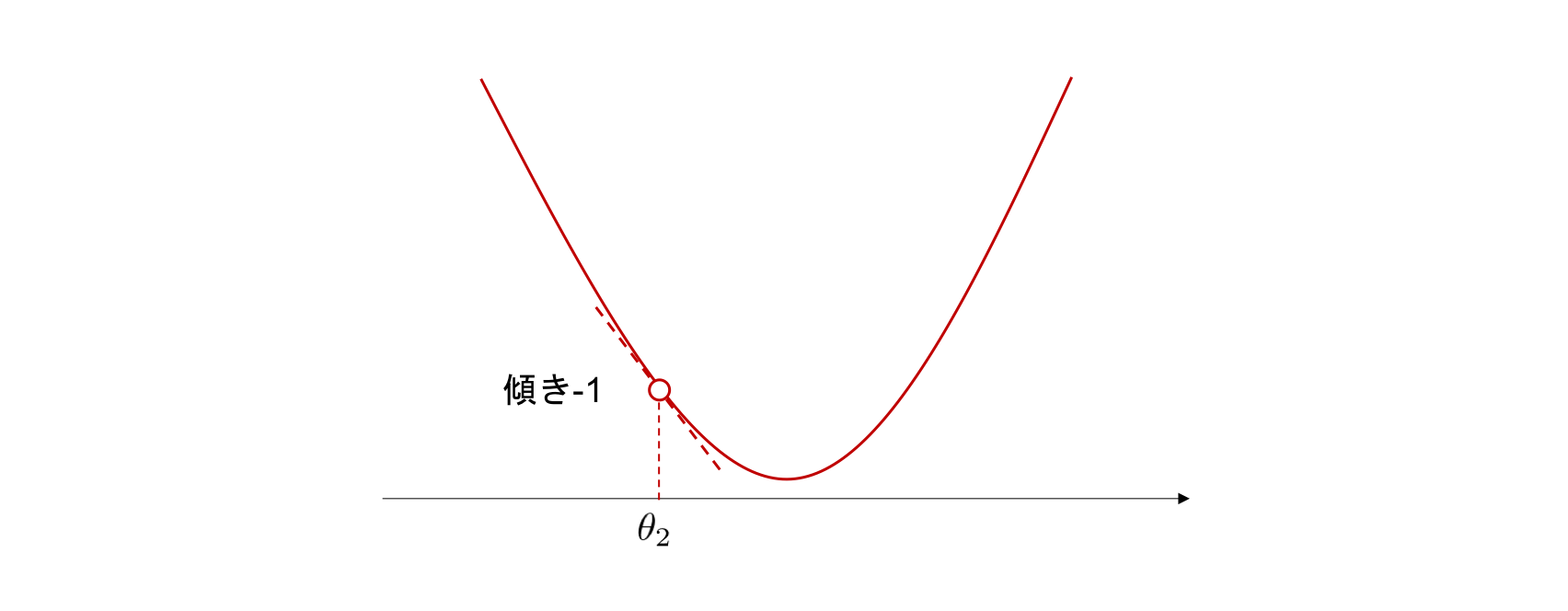



グラフ 勾配 意味



Jbrxmnmebqktgm
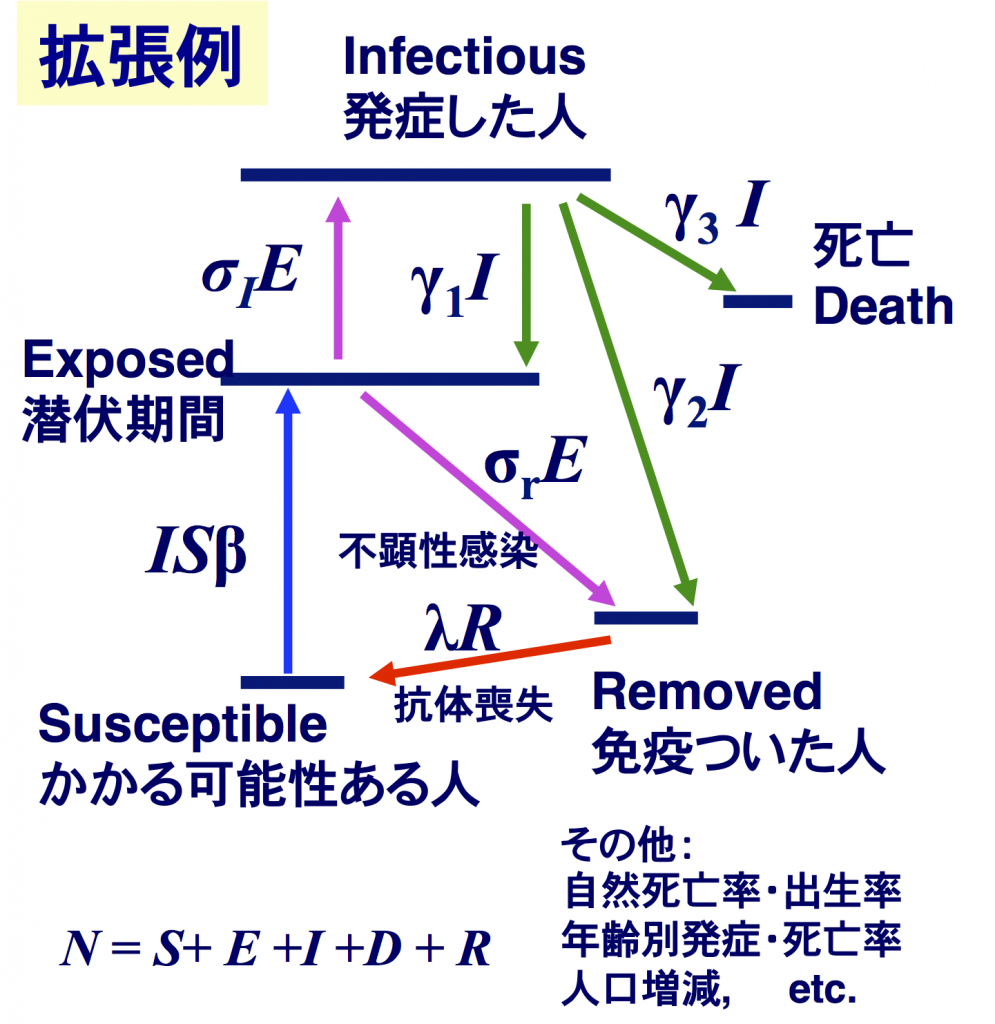



この感染は拡大か収束か 再生産数 R の物理的意味と決定 単純なモデル方程式に基づく行動変容の判断のために Rad It21
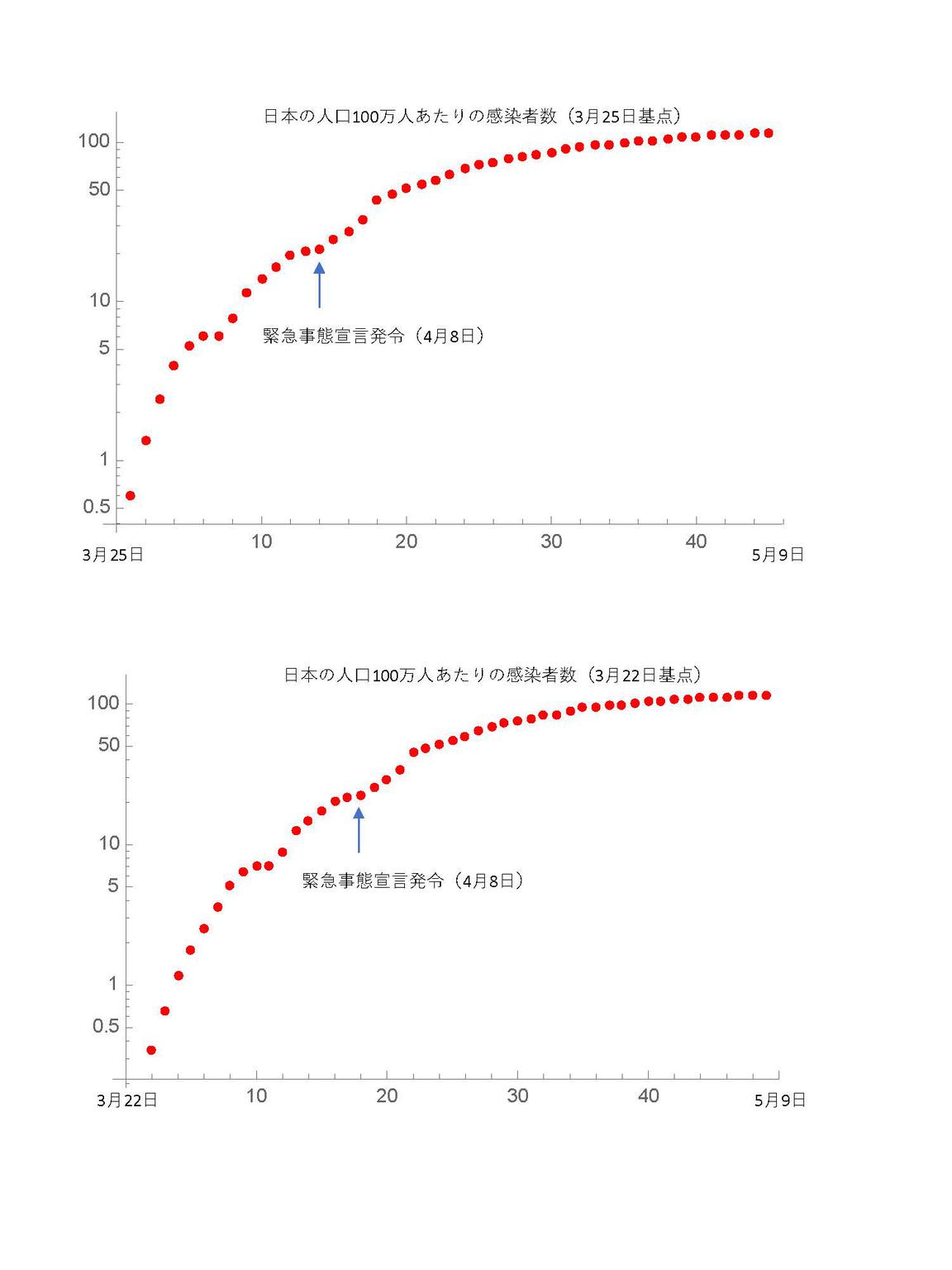



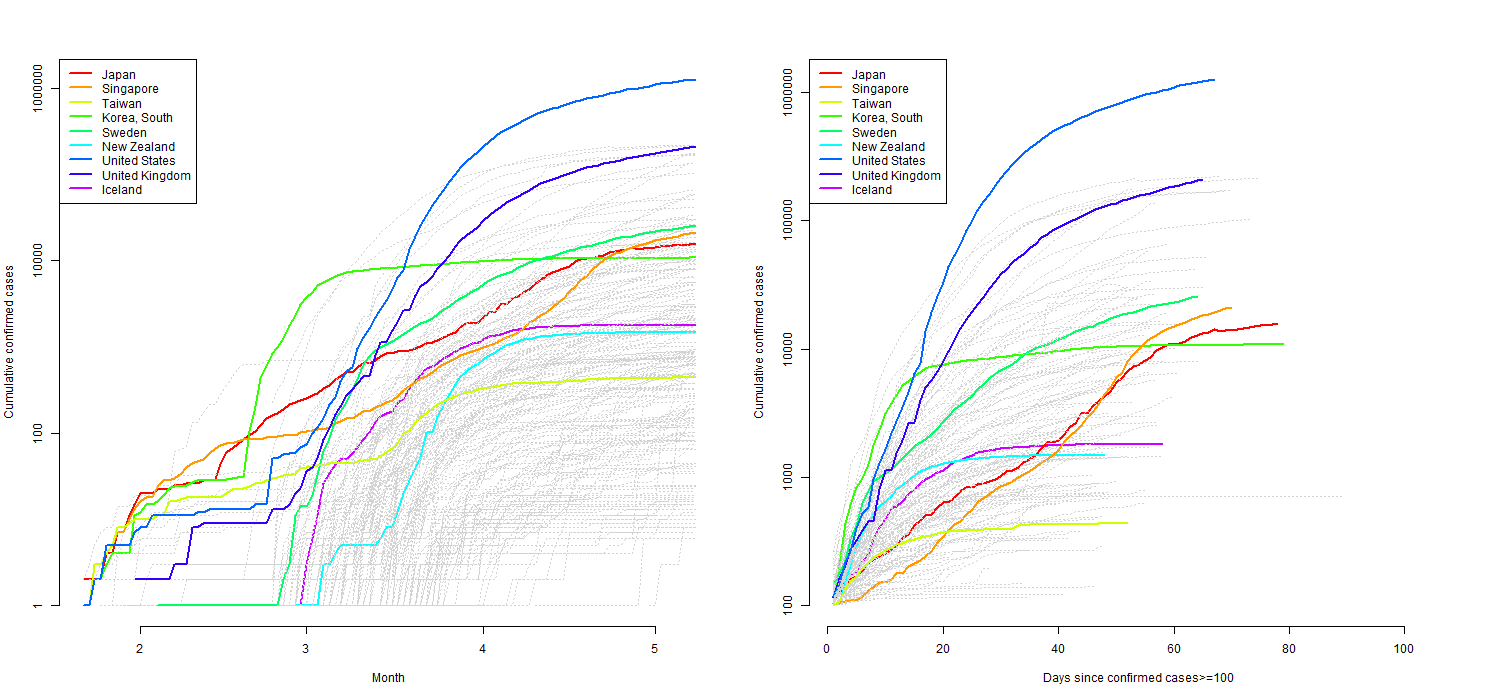
人口あたりの新型コロナウイルス感染者数の推移 世界 国別




11 号 乗法九九学習具 Astamuse



公開特許公報




18 号 計算装置及びサンプリング方法 Astamuse



ただのつぶやき




Pdf A Prediction Of Turbulence In Steep Slope Flow With Vegetation By K E Turbulent Model
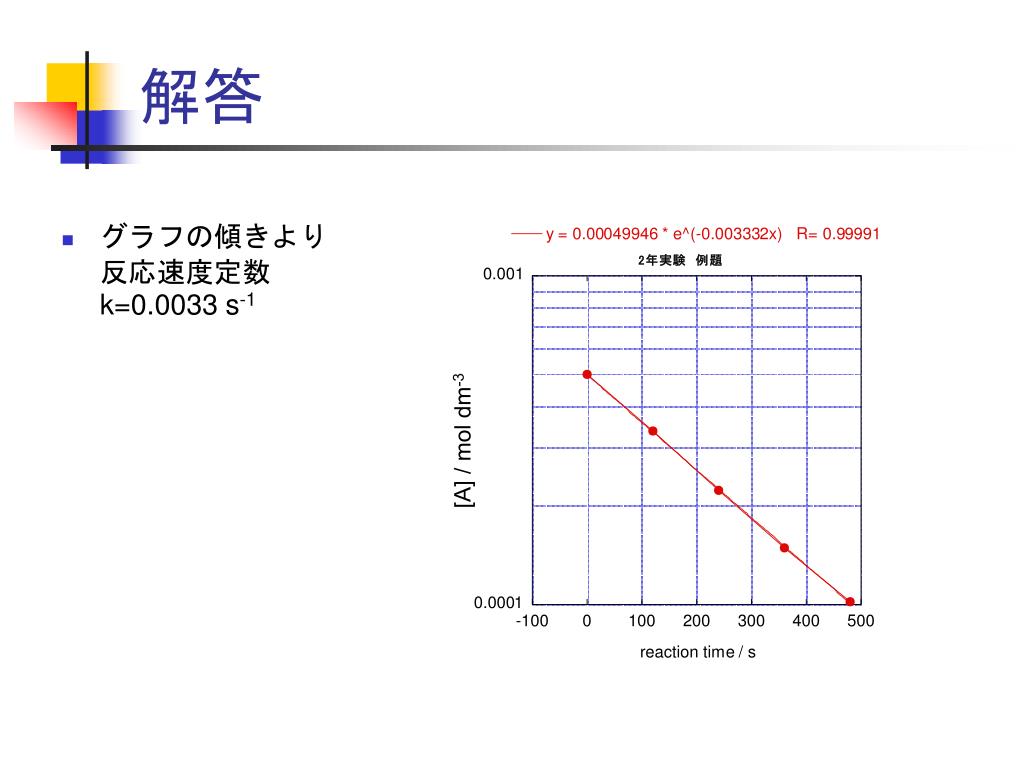



Ppt グルコースの変旋光 Powerpoint Presentation Free Download Id
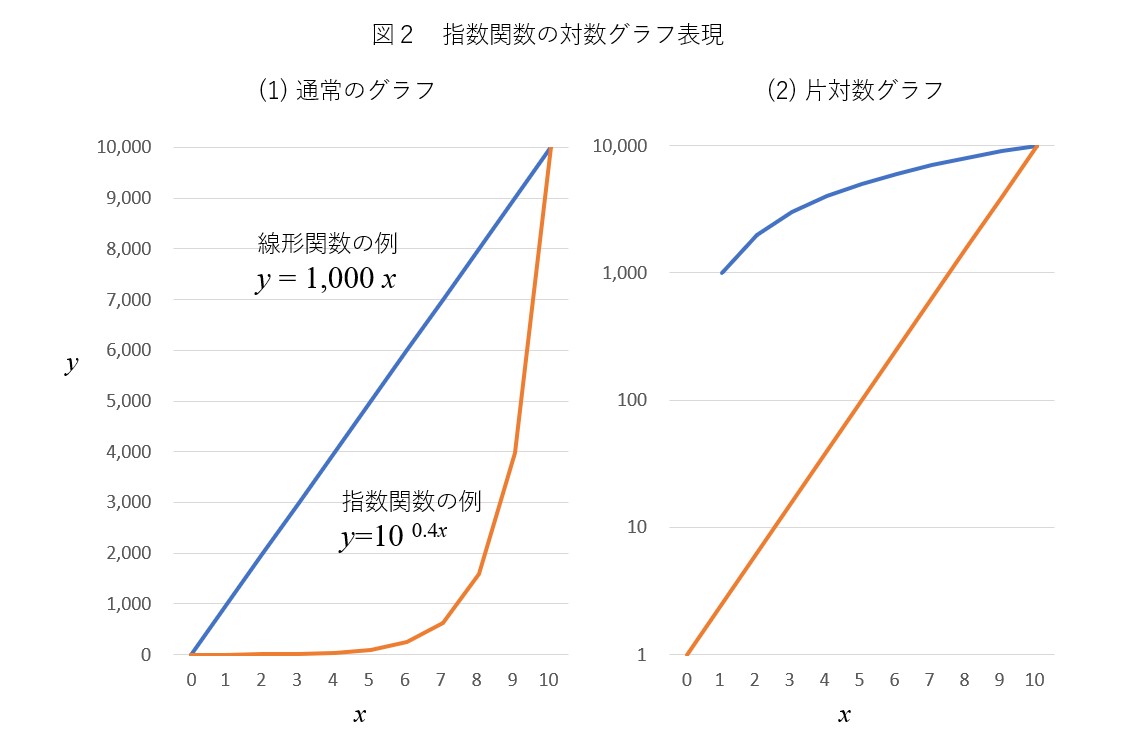



指数 関数 的 増加 新型コロナウイルスの感染者数は かくして指数関数的に 爆発的増加 する
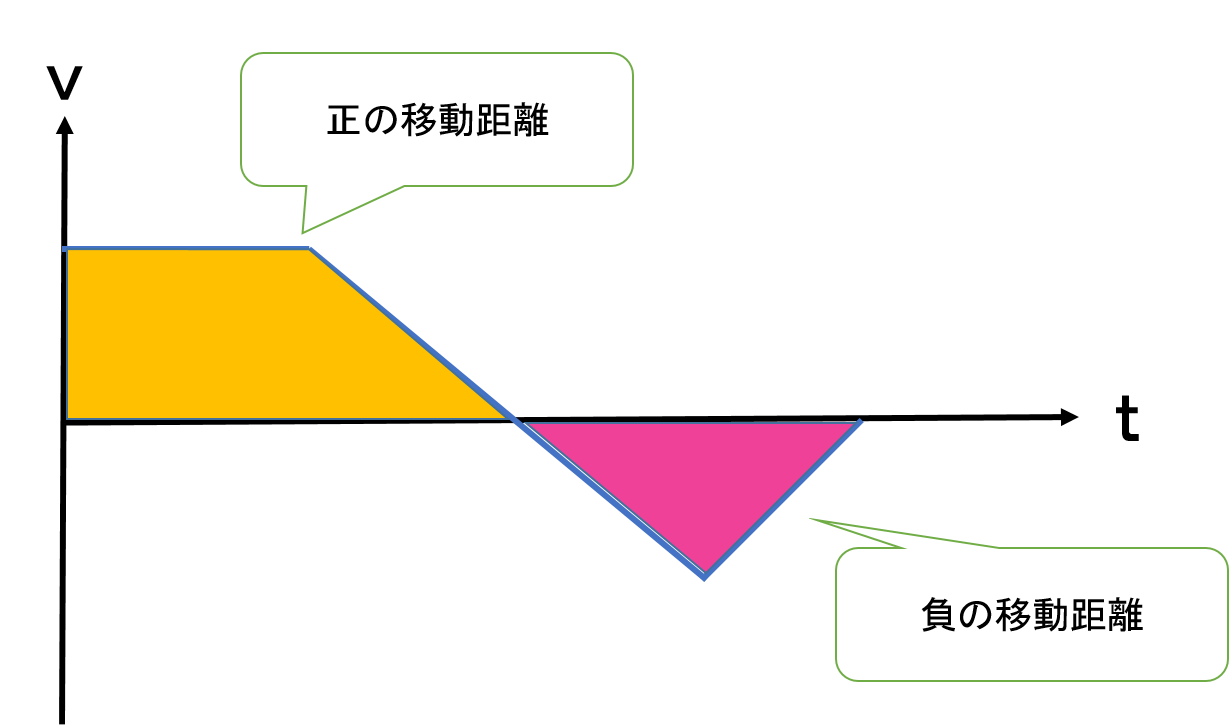



グラフ 勾配 意味




グーテンベルグ リヒター則 Wikipedia




11 号 乗法九九学習具 Astamuse




Jpa Dosage Form Containing Oxycodone And Naloxone Google Patents



19 Ncovについてのメモとリンク




片対数グラフとは何か Training Day
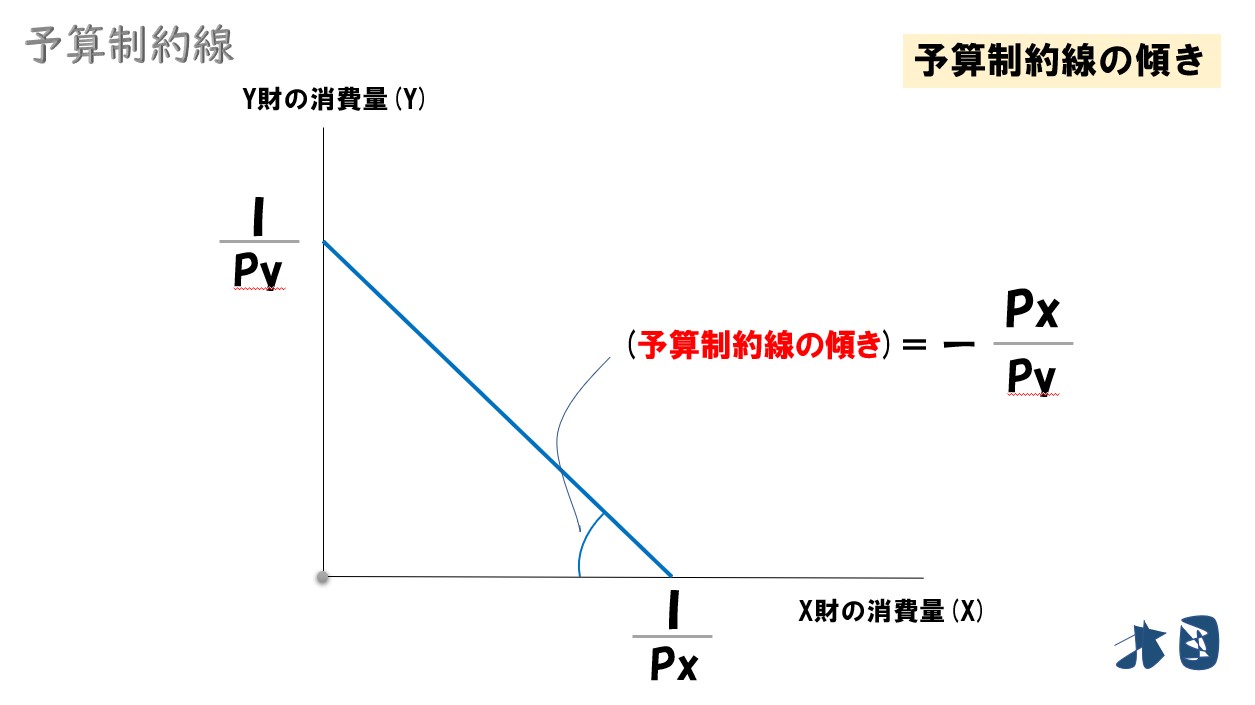



グラフ 勾配 意味



Ew 91回基礎完成
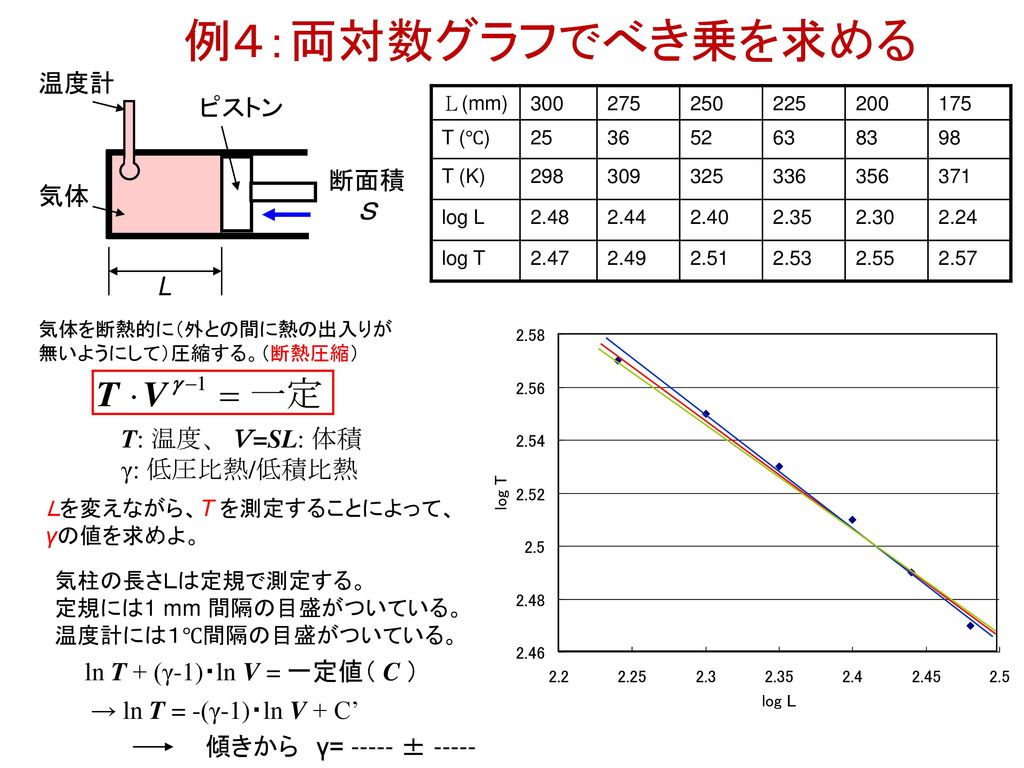



国際物理オリンピック実験試験のシラバス 1 標準的な実験器具 装置が使える マニュアル無しで使える Ppt Download
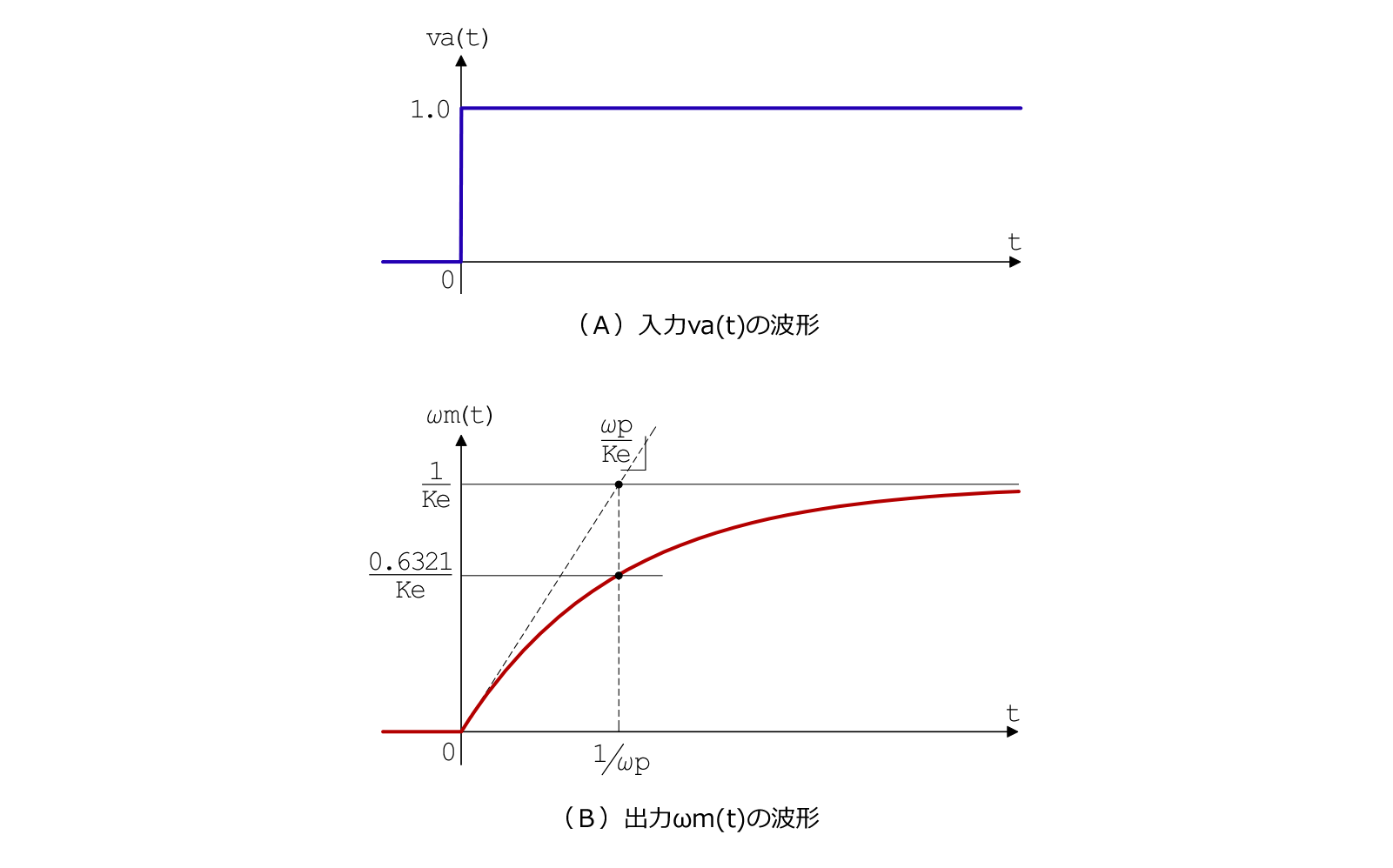



ただのつぶやき



ボード線図
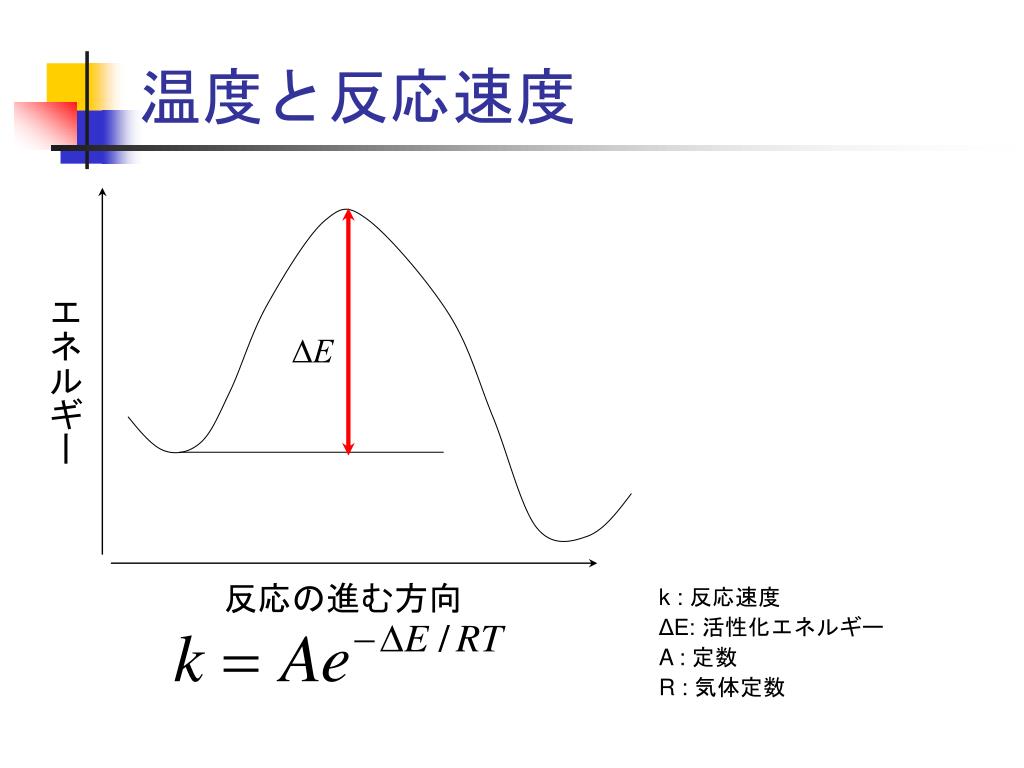



Ppt グルコースの変旋光 Powerpoint Presentation Free Download Id
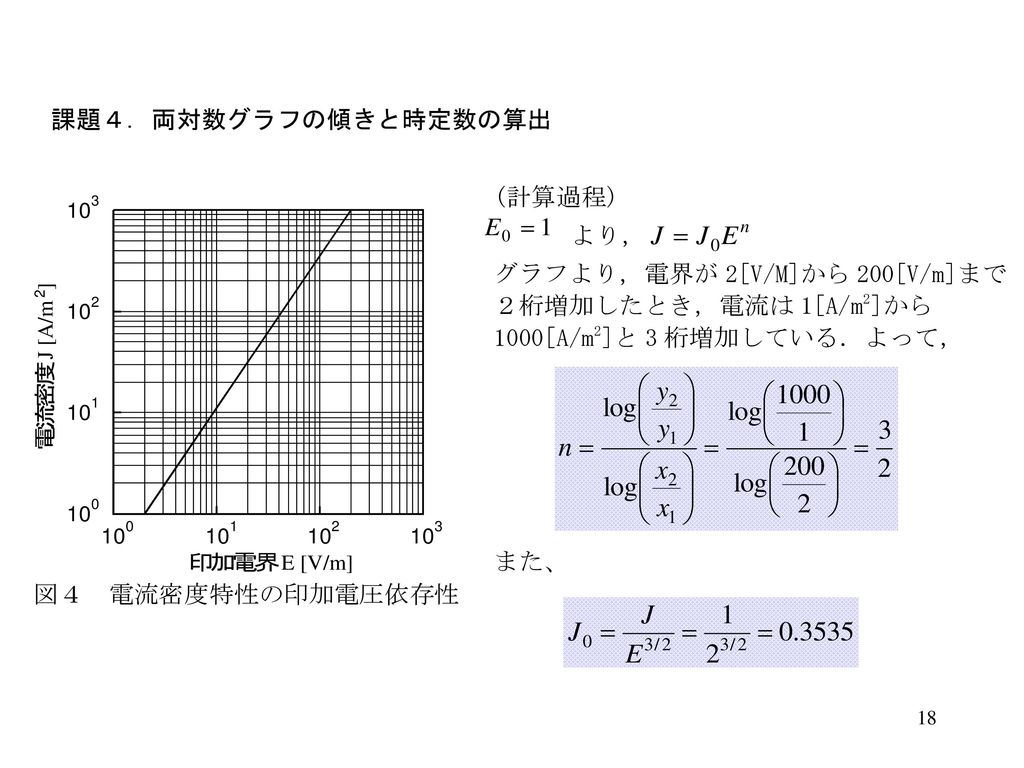



電気基礎実験 グラフ処理 Ppt Download
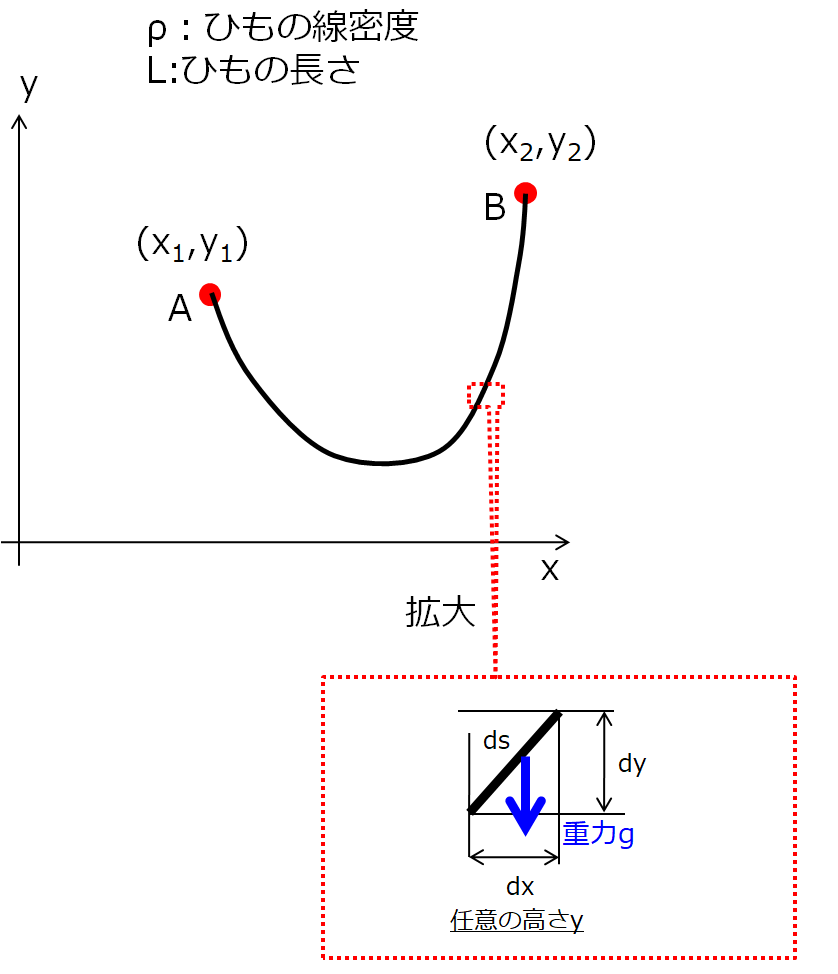



ラグランジュ未定乗数法 実現可能な状態 解析力学とのつながり 宇宙に入ったカマキリ
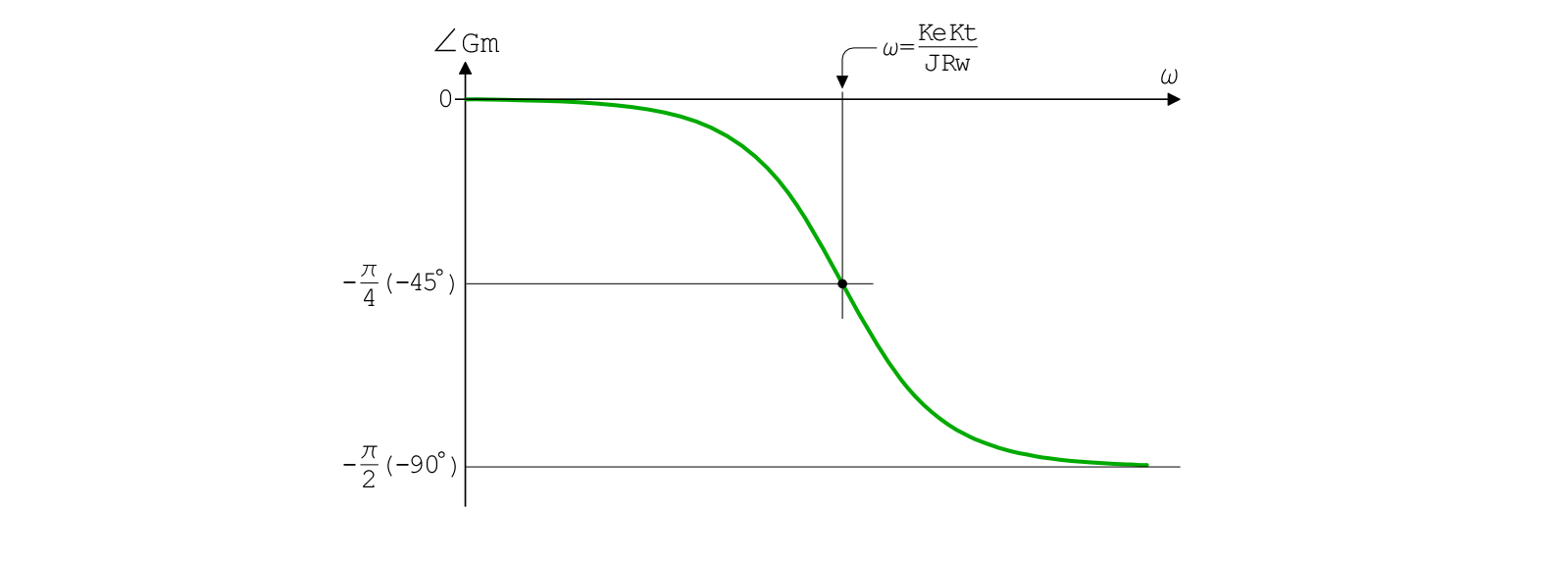



ただのつぶやき




ロジスティック方程式 Wikipedia
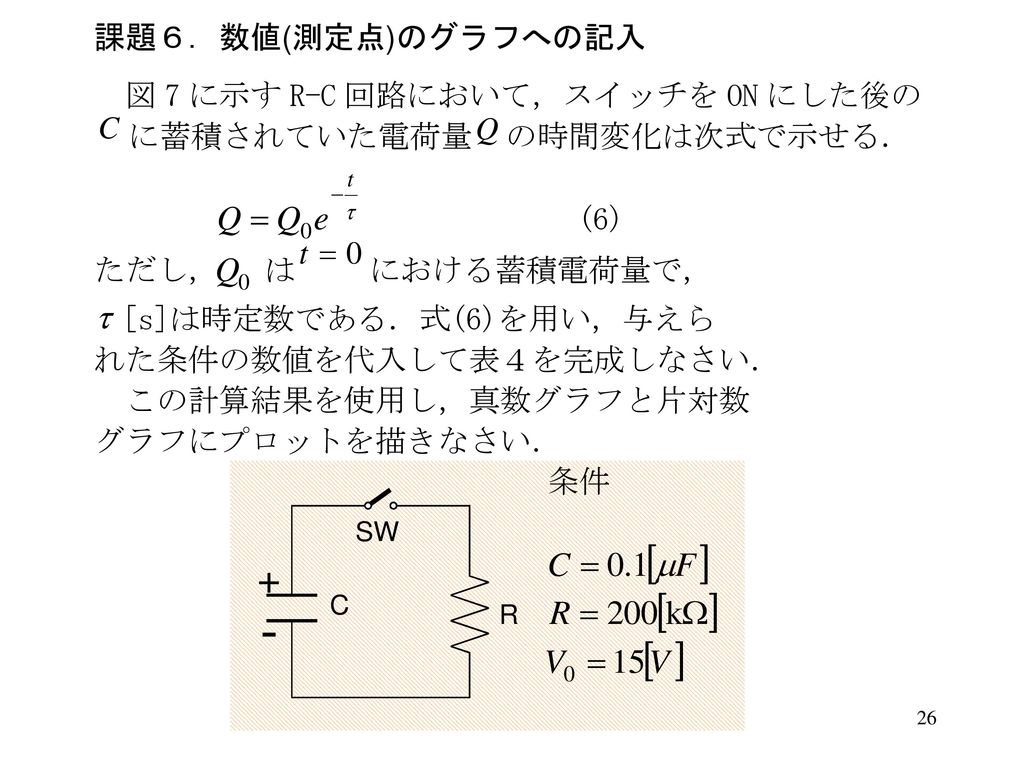



電気基礎実験 グラフ処理 Ppt Download




高校生からわかる片対数グラフと両対数グラフを使うと直線になる理由 宇宙に入ったカマキリ



公開特許公報
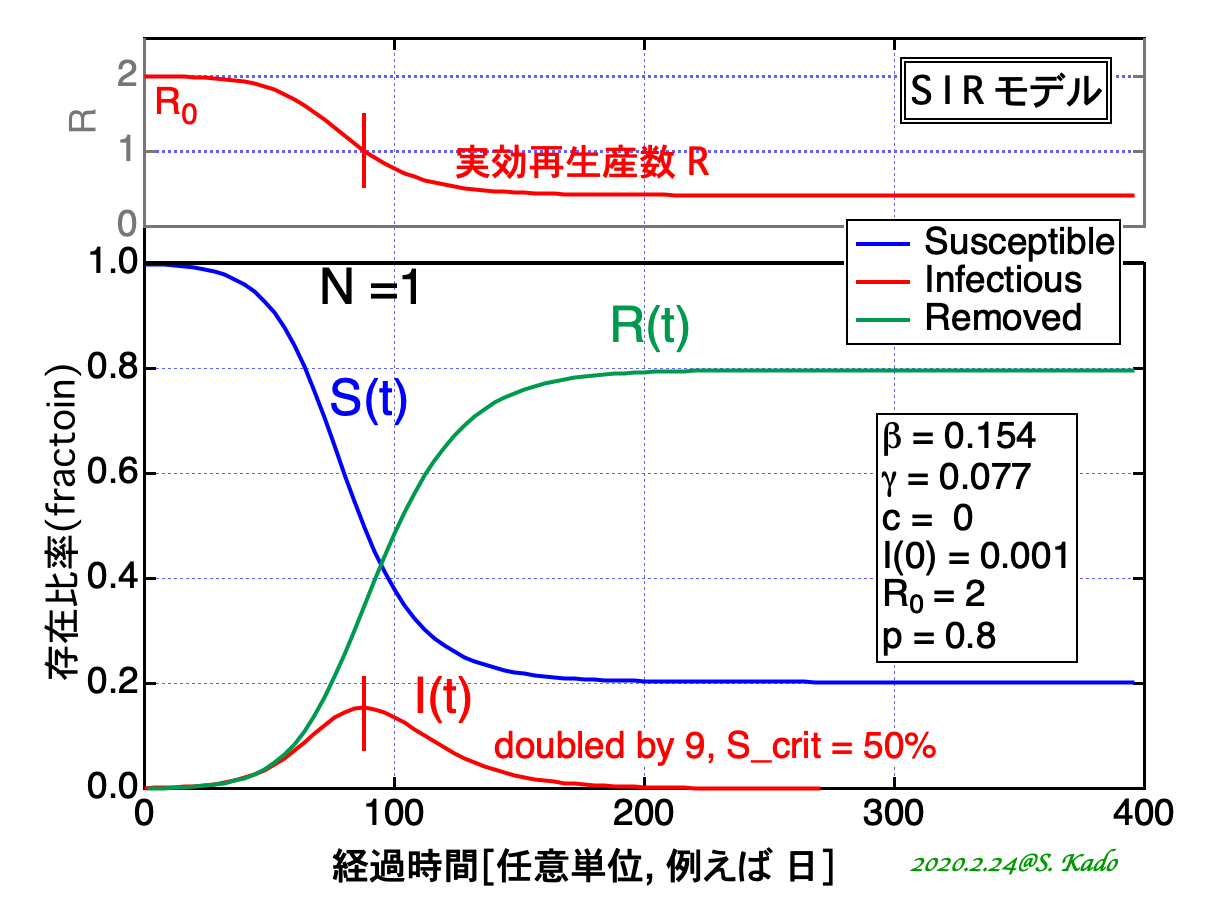



この感染は拡大か収束か 再生産数 R の物理的意味と決定 単純なモデル方程式に基づく行動変容の判断のために Rad It21
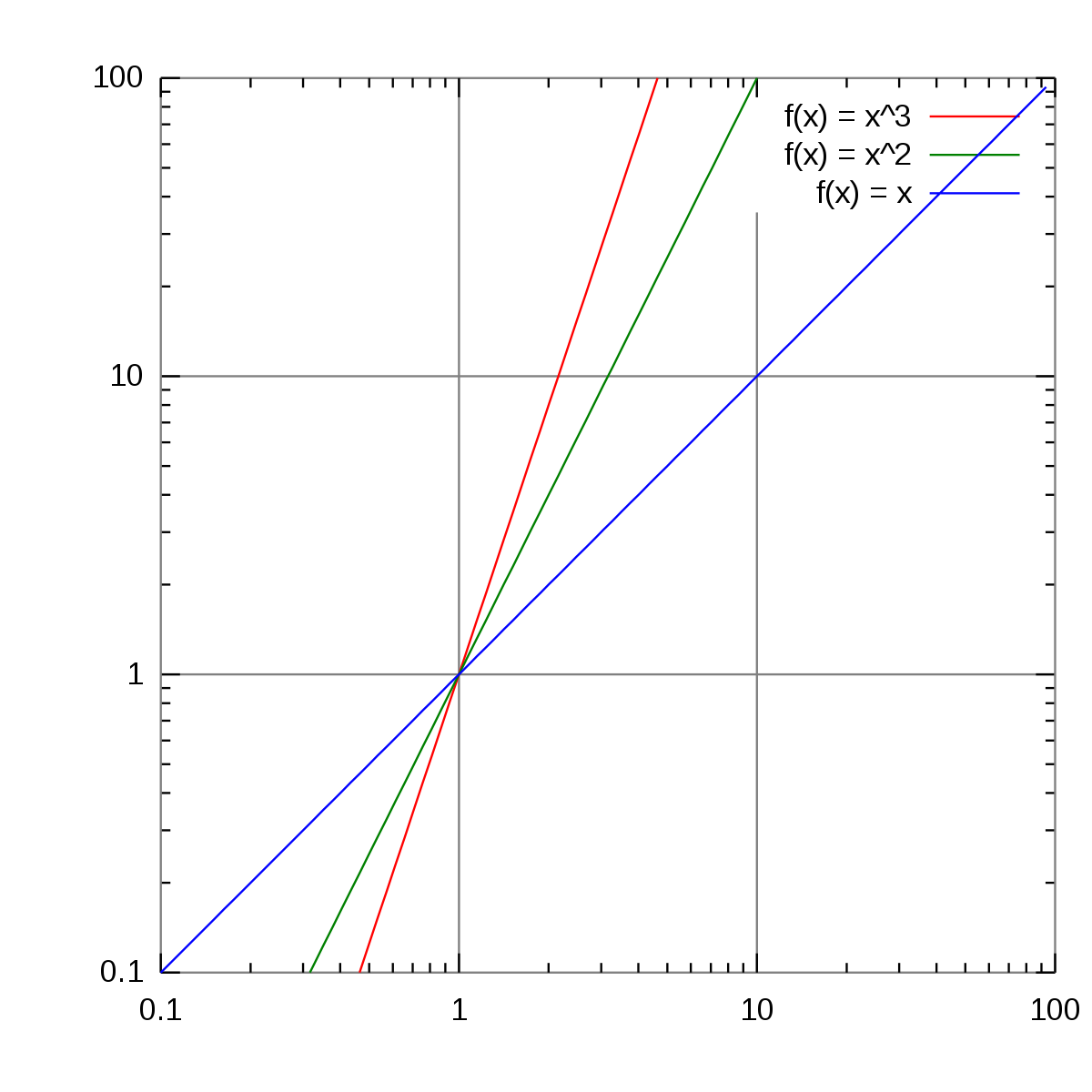



両対数グラフ Wikipedia
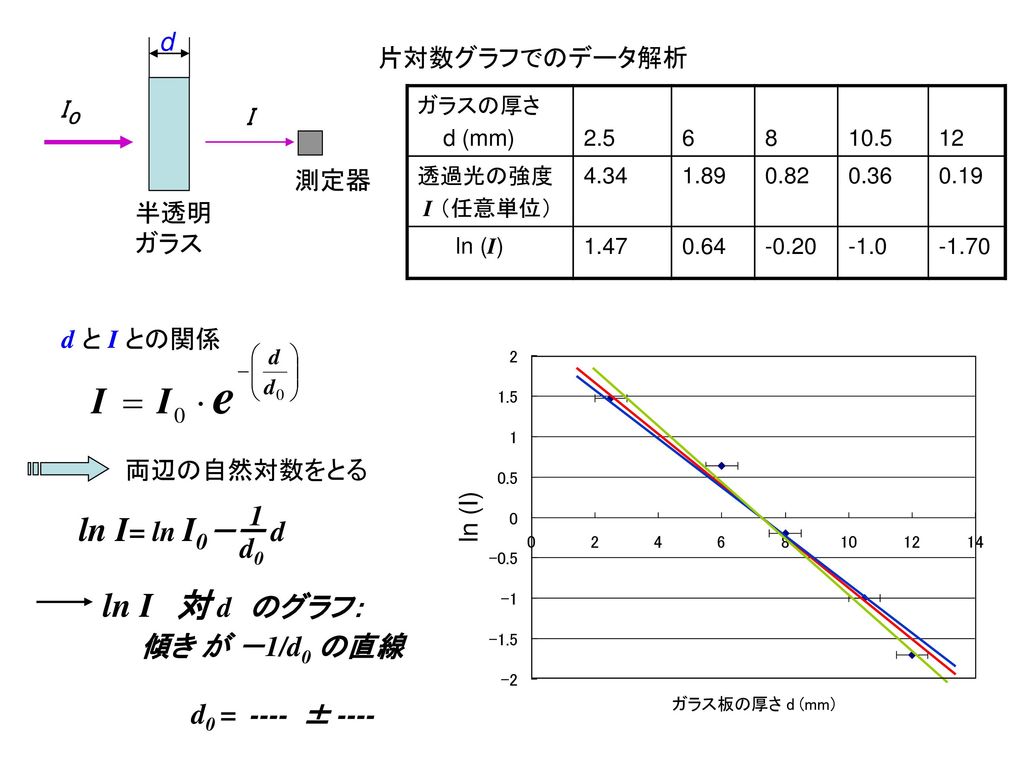



国際物理オリンピック実験試験のシラバス 1 標準的な実験器具 装置が使える マニュアル無しで使える Ppt Download



材料力学のカステリアーノの定理について 写真のb点でのたわみを求 Yahoo 知恵袋



公開特許公報



0 件のコメント:
コメントを投稿